题目内容
如图,平行四边形ABCD中,AC=4cm,BC=5cm,CD=3cm,则?ABCD的面积__.
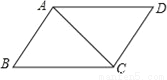
 12cm2
【解析】 ∵四边形ABCD是平行四边形,
∴AB=CD=3cm,
∵AC=4cm,BC=5cm,
∴AC2+AB2=AC2,
∴△ABC是直角三角形,
∴S△ABC=×3×4=6cm2,
∴则ABCD的面积=2×6=12cm2.
12cm2
【解析】 ∵四边形ABCD是平行四边形,
∴AB=CD=3cm,
∵AC=4cm,BC=5cm,
∴AC2+AB2=AC2,
∴△ABC是直角三角形,
∴S△ABC=×3×4=6cm2,
∴则ABCD的面积=2×6=12cm2.
练习册系列答案
相关题目
如图所示,已知六边形ABCDEF中,∠A=∠B=∠C=∠D=∠E=∠F=120°.试说明AB+BC=EF+ED.
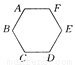
 见解析
【解析】分析:分别延长AB、DC相交于点M,延长AF、DE相交于点N,通过作辅助线我们可以得到∠MBC=∠MCB=60°,再结合三角形内角和定理即可判断△BMC是等边三角形,同理还可以得出△EFN是等边三角形;由“两组对角分别相等的四边形是平行四边形”可知四边形AMDN是平行四边形,从而可以得到AM=DN即可得出结果.
本题解析:分别延长AB、DC相交于点M,延长AF、DE相交...
见解析
【解析】分析:分别延长AB、DC相交于点M,延长AF、DE相交于点N,通过作辅助线我们可以得到∠MBC=∠MCB=60°,再结合三角形内角和定理即可判断△BMC是等边三角形,同理还可以得出△EFN是等边三角形;由“两组对角分别相等的四边形是平行四边形”可知四边形AMDN是平行四边形,从而可以得到AM=DN即可得出结果.
本题解析:分别延长AB、DC相交于点M,延长AF、DE相交... 某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活的情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
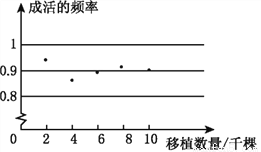
(1)这种树苗成活的频率稳定在___________,成活的概率估计值为___________.
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活___________万棵.
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
 (1)0.9附近,0.9;(2)①4.5,15万棵.
【解析】(1)由图可知,成活概率在0.9上下波动,故可估计这种树苗成活的频率稳定在0.9,成活的概率估计值为0.9;
(2)①5×成活率即为所求的成活的树苗棵树;
②方法1:利用成活率求得需要树苗棵树,减去已移植树苗数即为所求的树苗的棵树;
方法2:设还需移植这种树苗万棵,根据成活率及成活总数列出方程即可。
(1)0.9附近,0.9;(2)①4.5,15万棵.
【解析】(1)由图可知,成活概率在0.9上下波动,故可估计这种树苗成活的频率稳定在0.9,成活的概率估计值为0.9;
(2)①5×成活率即为所求的成活的树苗棵树;
②方法1:利用成活率求得需要树苗棵树,减去已移植树苗数即为所求的树苗的棵树;
方法2:设还需移植这种树苗万棵,根据成活率及成活总数列出方程即可。 下列命题中,其逆命题成立的是__.(只填写序号)
①同旁内角互补,两直线平行;
②如果两个角是直角,那么它们相等;
③如果两个实数相等,那么它们的平方相等;
④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
 ①④
【解析】把一个命题的条件和结论互换就得到它的逆命题,再分析逆命题是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案。
①两直线平行,同旁内角互补,正确;
②如果两个角相等,那么它们是直角,错误;
③如果两个实数的平方相等,那么这两个实数相等,错误;
④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形,正确.
...
①④
【解析】把一个命题的条件和结论互换就得到它的逆命题,再分析逆命题是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案。
①两直线平行,同旁内角互补,正确;
②如果两个角相等,那么它们是直角,错误;
③如果两个实数的平方相等,那么这两个实数相等,错误;
④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形,正确.
... 已知:如图,在?ABCD中,∠ADC,∠DAB的平分线DF,AE分别与线段BC相交于点F,E,DF与AE相交于点G.
(1)求证:AE⊥DF;
(2)若AD=10,AB=6,AE=4,求DF的长.
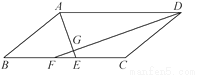
 (1)证明见解析;(2).
【解析】试题分析:(1)根据平行四边形的性质和平行线的性质推出∠ADC+∠DAB=180°,根据角平分线得到∠ADF+∠DAE=(∠ADC+∠DAB)=90°,即可求出结论;
(2)过点D作DH∥AE,交BC的延长线于点H,得到平行四边形AEHD,求出DH=AE=4,EH=AD=10,根据平行四边形的性质和平行线的性质推出DC=FC,AB=EB,求出BF、F...
(1)证明见解析;(2).
【解析】试题分析:(1)根据平行四边形的性质和平行线的性质推出∠ADC+∠DAB=180°,根据角平分线得到∠ADF+∠DAE=(∠ADC+∠DAB)=90°,即可求出结论;
(2)过点D作DH∥AE,交BC的延长线于点H,得到平行四边形AEHD,求出DH=AE=4,EH=AD=10,根据平行四边形的性质和平行线的性质推出DC=FC,AB=EB,求出BF、F... 在平行四边形ABCD中,∠B=60°,那么下列各式中,不能成立的是( )
A.∠D=60°
B.∠A=120°
C.∠C+∠D=180°
D.∠C+∠A=180°
 D
【解析】∵四边形ABCD是平行四边形,∴∠D=∠B=60°.故A正确;∵AD∥BC,∴∠C+∠D=180°,故C正确;∵AD∥BC,∴∠A+∠B=180°,∴∠A=180°-∠B=120°,故B正确;∵四边形ABCD是平行四边形,∴∠C=∠A=120°,故D不正确,故选D.
D
【解析】∵四边形ABCD是平行四边形,∴∠D=∠B=60°.故A正确;∵AD∥BC,∴∠C+∠D=180°,故C正确;∵AD∥BC,∴∠A+∠B=180°,∴∠A=180°-∠B=120°,故B正确;∵四边形ABCD是平行四边形,∴∠C=∠A=120°,故D不正确,故选D. 为了了解参加某运动会的2000名运动员的年龄情况,从中抽查了100名运动员的年龄,“某运动员被抽到”这一事件是______事件.
 随机.
【解析】由题意知是从2000名运动员的年龄中抽取100名运动员的年龄,每一名运动员被投到的频率为,即为,所以某运动员被抽到这一事件是随机事件.
随机.
【解析】由题意知是从2000名运动员的年龄中抽取100名运动员的年龄,每一名运动员被投到的频率为,即为,所以某运动员被抽到这一事件是随机事件. 下列条形中的能代圆形图所表示的数据( )

A. 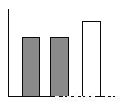 B.
B. 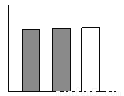 C.
C. 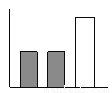 D.
D. 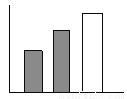
 C
【解析】由图知,阴影部分与空白部分面积相等,在给出的四个选项中,只有C中有阴影的两个矩形面积之和等于空白矩形面积.
故选C.
C
【解析】由图知,阴影部分与空白部分面积相等,在给出的四个选项中,只有C中有阴影的两个矩形面积之和等于空白矩形面积.
故选C. 关于中心对称的两个图形的关系是___________
 全等
【解析】关于中心对称的两个图形是全等图形.
故答案:全等.
全等
【解析】关于中心对称的两个图形是全等图形.
故答案:全等. 
