题目内容
如图，△ACE是以平行四边形ABCD的对角线AC为边的等边三角形，点C与点E关于x轴对称，CE交x轴于点H．若E点的坐标是(7，一3
)，则D点的坐标是__________．
(5，0)
【解析】试题分析：如图，设EC与x轴交于点Q,由点C与点E关于x轴对称可得出（7，3），CE=6，因△ACE是以□ABCD的对角线AC为边的等边三角形，所以AC=CE=6，根据勾股定理即可求出AQ的长为9，又因OQ=7，所以OA=DQ=2，再求得OD=5，即可得D点的坐标是（5,0）．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
我们知道过n边形的一个顶点可以做（n－3）条对角线，这（n－3）条对角线把三角形分割成（n－2）个三角形，想一想这是为什么？如图1．
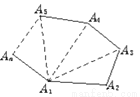
图1
如图2，在n边形的边上任意取一点，连结这点与各顶点的线段可以把n边形分成几个三角形？
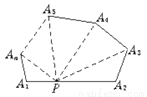
图2
想一想，利用这两个图形，怎样证明多边形的内角和定理．
n-2．想一想见解析
【解析】分析：本题主要考查利用三角形内角和定理来证明多边形的内角和定理，从多边形的一个顶点出发引对角线，则把n边形分成（n-2)个三角形从而证明多边形的内角和定理.
本题解析：
(1)因为对角线是连结不相邻的两个顶点之间的线段，每一个顶点都有两个相邻的顶点，所以有（n-3)条对角线，三条边组成一个三角形，(1)图可分成(n-2)个三角形,
(2)图可分... 计算：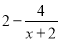 
= ．
【解析】试题分析：原式＝
＝
＝．
故答案为： ． 如图，圆柱形玻璃杯，高为12cm，底面周长为18cm，在杯内离杯底3cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为__cm．
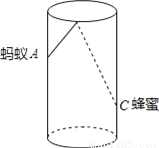
5
【解析】试题分析：沿过A的圆柱的高剪开，得出矩形EFGH，过C作CQ⊥EF于Q，作A关于EH的对称点，连接交EH于P，连接AP，
则AP+PC就是蚂蚁到达蜂蜜的最短距离，∵AE= , =AP，∴AP+PC= +PC= ,∵CQ=×18=9cm， =12-4+4=12cm，在Rt△中，由勾股定理得： ==15cm．故答案为15． 满足下列条件的三角形不一定是直角三角形的是（ ）
A. 三条边的比为5：12：13
B. 三个角的度数比为2：3：5
C. 有一边等于另一条边的一半
D. 三角形的三边长分别是24、25和7
C
【解析】A、因为其符合勾股定理的逆定理，所以是直角三角形，故正确；
B、因为根据三角形内角和定理可求出三个角分别为36度，54度，90度，所以是直角三角形，故正确；
C、因为根据三角形内角和公式得三个角中没有90°角，所以不是直角三角形，故不正确；
D、因为其符合勾股定理的逆定理，所以是直角三角形，故正确；
故选C． 在△MNB中，BN=6，点A，C，D分别在MB，NB，MN上，四边形ABCD为平行四边形，且∠NDC=∠MDA，则四边形ABCD的周长是（ ）
A．24 B．18 C．16 D．12
D
【解析】
在平行四边形ABCD中CD∥AB，AD∥BC，∴∠M=∠NDC，∠N=∠MDA，∵∠NDC=
∠MDA，∴∠M=∠N=∠NDC=∠MDA，∴MB=BN=6，CD=CN，AD=MA，∴四边形ABCD的周长=AB+BC+CD+AD=MA+AB+BC+CN=MB+BN=2BN=12． 从一副扑克牌中任取一张，则抽到红桃的频率与抽到黑桃的频率哪个大？抽到梅花与抽到大、小王的频率哪个大？
抽到红桃的可能性与抽到黑桃的频率一样大，而抽到梅花的频率大于抽到大、小王的频率.
【解析】试题分析: 本题考察可能性大小的应用，关键是根据各色扑克的张数求出各色扑克被抽到的频率是多少.
【解析】
一副扑克牌有54张，其中红桃、黑桃、梅花、方块各13张，大、小王各一张，所以，抽到红桃的的频率为，抽到黑桃的的频率为，抽到梅花的的频率为，抽到大、小王的的频率为. 所以抽到红桃的可能性与抽到... 今天下雨，两天后（ ）下雨.
A. 一定 B. 可能 C. 不可能 D. 以上都不对
B
【解析】今天下雨与两天后下雨不下雨没有任何关联.所以“两天后下雨”这是一个随机事件.
故选B. 关于中心对称的两个图形，对称点的连线经过__________
对称中心
【解析】关于中心对称的两个图形，对称点的连线经过对称中心.
故答案：对称中心.