在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A. 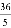 B.
B. 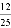 C.
C.  D.
D. 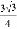
 A
【解析】试题分析:首先根据勾股定理可得:AB=,根据等面积法可得:点C到AB的距离为:(9×12)÷15=.
A
【解析】试题分析:首先根据勾股定理可得:AB=,根据等面积法可得:点C到AB的距离为:(9×12)÷15=. 如图,将边长为8㎝的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN的长是( )
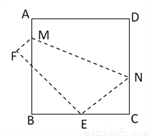
A. 3cm B. 4cm C. 5cm D. 6cm
 A
【解析】分析:根据折叠的性质,只要求出DN就可以求出NE,在直角△CEN中,若设CN=x,则DN=NE=8-x,CE=4cm,根据勾股定理就可以列出方程,从而解出CN的长.
解答:【解析】
设CN=xcm,则DN=(8-x)cm,由折叠的性质知EN=DN=(8-x)cm,
而EC=BC=4cm,在Rt△ECN中,由勾股定理可知EN2=EC2+CN2,即(8-x)2=16+x...
A
【解析】分析:根据折叠的性质,只要求出DN就可以求出NE,在直角△CEN中,若设CN=x,则DN=NE=8-x,CE=4cm,根据勾股定理就可以列出方程,从而解出CN的长.
解答:【解析】
设CN=xcm,则DN=(8-x)cm,由折叠的性质知EN=DN=(8-x)cm,
而EC=BC=4cm,在Rt△ECN中,由勾股定理可知EN2=EC2+CN2,即(8-x)2=16+x... 如图,在△ABC中,CA=CB,AD⊥BC,BE⊥AC,AB=5,AD=4,则AE=__.
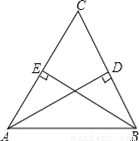
 3
【解析】试题分析:∵在△ABC中,CA=CB,AD⊥BC,BE⊥AC,∴△ABD≌△BAE(AAS)。∴AD=BE=4。
∵AB=5,∴。
3
【解析】试题分析:∵在△ABC中,CA=CB,AD⊥BC,BE⊥AC,∴△ABD≌△BAE(AAS)。∴AD=BE=4。
∵AB=5,∴。 下列命题中,其逆命题成立的是__.(只填写序号)
①同旁内角互补,两直线平行;
②如果两个角是直角,那么它们相等;
③如果两个实数相等,那么它们的平方相等;
④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
 ①④
【解析】把一个命题的条件和结论互换就得到它的逆命题,再分析逆命题是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案。
①两直线平行,同旁内角互补,正确;
②如果两个角相等,那么它们是直角,错误;
③如果两个实数的平方相等,那么这两个实数相等,错误;
④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形,正确.
...
①④
【解析】把一个命题的条件和结论互换就得到它的逆命题,再分析逆命题是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案。
①两直线平行,同旁内角互补,正确;
②如果两个角相等,那么它们是直角,错误;
③如果两个实数的平方相等,那么这两个实数相等,错误;
④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形,正确.
... 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是__.
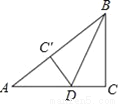
 6cm2
【解析】试题分析:先根据勾股定理得到AB=10cm,再根据折叠的性质得到DC=DC′,BC=BC′=6cm,则AC′=4cm,设DC=xcm,在Rt△ADC′中根据勾股定理列方程求得x的值,然后根据三角形的面积公式计算即可.
∵∠C=90°,BC=6cm,AC=8cm,
∴AB=10cm,
∵将△BCD沿BD折叠,使点C落在AB边的C′点,
∴△BCD≌△B...
6cm2
【解析】试题分析:先根据勾股定理得到AB=10cm,再根据折叠的性质得到DC=DC′,BC=BC′=6cm,则AC′=4cm,设DC=xcm,在Rt△ADC′中根据勾股定理列方程求得x的值,然后根据三角形的面积公式计算即可.
∵∠C=90°,BC=6cm,AC=8cm,
∴AB=10cm,
∵将△BCD沿BD折叠,使点C落在AB边的C′点,
∴△BCD≌△B... 如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为__cm.
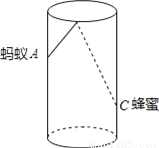
 5
【解析】试题分析:沿过A的圆柱的高剪开,得出矩形EFGH,过C作CQ⊥EF于Q,作A关于EH的对称点,连接交EH于P,连接AP,
则AP+PC就是蚂蚁到达蜂蜜的最短距离,∵AE= , =AP,∴AP+PC= +PC= ,∵CQ=×18=9cm, =12-4+4=12cm,在Rt△中,由勾股定理得: ==15cm.故答案为15.
5
【解析】试题分析:沿过A的圆柱的高剪开,得出矩形EFGH,过C作CQ⊥EF于Q,作A关于EH的对称点,连接交EH于P,连接AP,
则AP+PC就是蚂蚁到达蜂蜜的最短距离,∵AE= , =AP,∴AP+PC= +PC= ,∵CQ=×18=9cm, =12-4+4=12cm,在Rt△中,由勾股定理得: ==15cm.故答案为15. 如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C=__度.
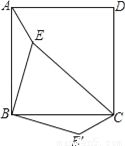
 135
【解析】试题分析:首先根据旋转的性质得出,△EBE′是直角三角形,进而得出∠BEE′=∠BE′E=45°,即可得出答案.
【解析】
连接EE′
∵△ABE绕点B顺时针旋转90°到△CBE′
∴∠EBE′是直角,∴△EBE′是直角三角形,
∵△ABE与△CE′B全等
∴BE=BE′=2,∠AEB=∠BE′C
∴∠BEE′=∠BE′E=45°,
...
135
【解析】试题分析:首先根据旋转的性质得出,△EBE′是直角三角形,进而得出∠BEE′=∠BE′E=45°,即可得出答案.
【解析】
连接EE′
∵△ABE绕点B顺时针旋转90°到△CBE′
∴∠EBE′是直角,∴△EBE′是直角三角形,
∵△ABE与△CE′B全等
∴BE=BE′=2,∠AEB=∠BE′C
∴∠BEE′=∠BE′E=45°,
... 如图,BC=4cm,AB=3cm,AF=12cm,AC⊥AF,正方形CDEF的面积是169cm2,试判断△ABC的形状?
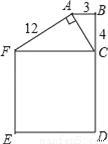
 △ABC是直角三角形.
【解析】分析:首先根据正方形的面积求出FC的长,再在Rt△ACF中利用勾股定理求出AC的长,然后根据勾股定理逆定理证明∠B=90°即可.
本题解析:
∵正方形CDEF的面积是169 cm2,
∴FC=13 cm
在Rt△ACF中,由勾股定理得,
AC2=CF2﹣AF2=132﹣122=25,
在△ABC中,因为AB2+BC2=32+...
△ABC是直角三角形.
【解析】分析:首先根据正方形的面积求出FC的长,再在Rt△ACF中利用勾股定理求出AC的长,然后根据勾股定理逆定理证明∠B=90°即可.
本题解析:
∵正方形CDEF的面积是169 cm2,
∴FC=13 cm
在Rt△ACF中,由勾股定理得,
AC2=CF2﹣AF2=132﹣122=25,
在△ABC中,因为AB2+BC2=32+... 如图所示、△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上.
(1)求证:△AOC≌△BOD;
(2)若AD=1,BD=2,求CD的长.
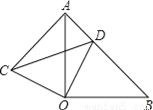
 (1)证明见解析;(2)CD的长为.
【解析】(1)证明:如右图1,
,
又,
(2)由有: , ,
,故
(1)证明见解析;(2)CD的长为.
【解析】(1)证明:如右图1,
,
又,
(2)由有: , ,
,故 在△ABC中,BC=a,AC=b,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边分别为6、8、9时,△ABC为 三角形;当△ABC三边分别为6、8、11时,△ABC为 三角形.
(2)猜想,当a2+b2 c2时,△ABC为锐角三角形;当a2+b2 c2时,△ABC为钝角三角形.
(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.
 【解析】
(1)锐角;钝角。
(2)>;<。
(3)①当4≤c<2时,这个三角形是锐角三角形;
②当c=2时,这个三角形是直角三角形;
③当2<c<6时,这个三角形是钝角三角形.。
【解析】
试题分析:(1)利用勾股定理列式求出两直角边为6、8时的斜边的值,然后作出判断即可:
∵两直角边分别为6、8时,斜边=10,
∴当△ABC三边分别为6、8、9...
【解析】
(1)锐角;钝角。
(2)>;<。
(3)①当4≤c<2时,这个三角形是锐角三角形;
②当c=2时,这个三角形是直角三角形;
③当2<c<6时,这个三角形是钝角三角形.。
【解析】
试题分析:(1)利用勾股定理列式求出两直角边为6、8时的斜边的值,然后作出判断即可:
∵两直角边分别为6、8时,斜边=10,
∴当△ABC三边分别为6、8、9...