已知抛物线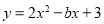
的对称轴是直线
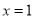，则
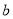的值为 ．
b=4
【解析】
试题分析：由抛物线的对称轴x=-和已知条件抛物线y=2-bx+3的对称轴是直线x=1，得到的等式，即可求出b的值． 某工厂有一种产品现在的年产量是20万件，计划今后两年增加产量，如果每年都比上一年的产量增加x倍，那么两年后这种产品的产量y将随计划所定的x的值而确定，那么y与x之间的关系应表示为_____．
y=20(x+1)2
【解析】∵某工厂一种产品的年产量是20件，每一年都比上一年的产品增加x倍，
∴一年后产品是：20（1+x），
∴两年后产品y与x的函数关系是：y=20（1+x）2．
故答案为：y=20（x+1）2. 如图所示，在同一平面直角坐标系中，作出①y=﹣3x2，②y=﹣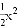
，③y=﹣x2的图象，则从里到外的三条抛物线对应的函数依次是______（填序号）
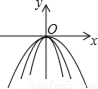
① ③ ②
【解析】①y=?3x²，②y=?x²，③y=?x²中,二次项系数a分别为?3、?、?1，
∵|?3|>|?1|>，∴抛物线②y=?x²的开口最宽,抛物线①y=?3x²的开口最窄。
故答案为：①③②。 将抛物线y=2（x﹣1）2+2向左平移3个单位，再向下平移4个单位，那么得到的抛物线的表达式为 ．
y=2﹣2
【解析】试题分析：按照“左加右减，上加下减”的规律可得抛物线y=2（x﹣1）2+2向左平移3个单位，再向下平移4个单位得到y=2（x﹣1+3）2+2﹣4=2（x+2）2﹣2．即可得抛物线的解析式为y=2（x+2）2﹣2． 如图，点A，B的坐标分别为（1， 4）和（4， 4），抛物线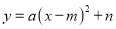
的顶点在线段AB上运动，与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为-3，则点D的横坐标最大值为_______。
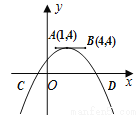
8
【解析】当抛物线y=a（x-m）2+n的顶点在线段AB的A点上时，点C的横坐标最小，把A（1，4）代入得：y=a（x-1）2+4，把C（-3，0）代入得：0=a（-3-1）2+4，解得：a=-，即：y=-（x-1）2+4，再根据题意知抛物线y=a（x-m）2+n的顶点在线段AB上运动，可得抛物线的a永远等于-，当抛物线的顶点运动到B时，D的横坐标最大，把a=-和B（4，4）代入y=a（x... 已知函数y=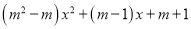
(1)若这个函数是一次函数，求m的值;
(2)若这个函数是二次函数，则m的值应怎样？
(1)、m=0；(2)、m≠0且m≠1.
【解析】试题分析：（1）由一次函数的定义求解；
（2）由二次函数的定义求解．
试题解析：（1）由一次函数的定义，得： ，解得m=0或m=1，又∵m﹣1≠0即m≠1；∴当m=0时，这个函数是一次函数；
（2）由二次函数的定义，得： ，解得且，∴当且时，这个函数是二次函数． 已知二次函数的图象以A（-1，4）为顶点，且过点B（2，-5）．
（1）求该二次函数的解析式；
（2）求该二次函数图象与坐标轴的交点坐标；
（1）二次函数的关系式是y=-（x+1）2+4；（2）交点坐标是（-3，0）、（1，0）
【解析】试题分析：
（1）由题意可设二次函数解析式为，代入点B的坐标（2，-5）求出的值，即可得到二次函数的解析式；
（2）在（1）中所求函数解析式中，由时，求得对应的函数值即可得到函数图象与轴的交点坐标；由可得一元二次方程，解方程即可求得二次函数的图象与轴的交点坐标.
试题解析：
... 二次函数y=ax2+bx+c的图象过A（﹣3，0），B（1，0），C（0，3），点D在函数图象上，点C，D是二次函数图象上的一对对称点，一次函数图象过点B，D，求：
（1）一次函数和二次函数的解析式；
（2）写出使一次函数值大于二次函数值的x的取值范围．
（1）y1=﹣x2﹣2x+3（2）x＜﹣2或x＞1．
【解析】
试题分析：（1）将A、B、C的坐标代入抛物线的解析式中即可求得二次函数的解析式，进而可根据抛物线的对称轴求出D点的坐标，再用待定系数法求出一次函数解析式；
（2）根据（1）画出函数图象，即可写出一次函数值大于二次函数值的x的取值范围．
【解析】
（1）二次函数y1=ax2+bx+c的图象经过点A（﹣3，0），... 广东特产专卖店销售龙眼干，其进价为每斤40元，按每斤60元出售，平均每天可售出100斤，后来经调查发现，单价每降低2元，则平均每天的销售量增加20斤．每斤降价多少元，每天销售额最大？
20元
【解析】
试题分析：根据题意可以列出销售额与销售单价之间的关系式，然后整理为顶点式，即可解答本题．
【解析】
设每斤降价x元，销售额为y元，
y=（60﹣x）（100+）=﹣10（x﹣25）2+12250，
∴当x＜25时，y随x的增大而增大，
∵60﹣40=20，
∴0≤x≤20，
∴当x=20时，y取得最大值，
即每斤降价20元时... 如图，抛物线y=﹣x2+3x+4与x轴交于点A，B，与y轴交于点C，P（m，n）为第一象限内抛物线上的一点，点D的坐标为（0，6）．
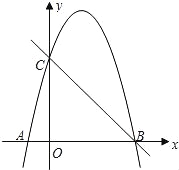
（1）OB=_________，抛物线的顶点坐标为_________________；
（2）当n=4时，求点P关于直线BC的对称点P′的坐标；
（3）是否存在直线PD，使直线PD所对应的一次函数随x的增大而增大？若存在，直接写出m的取值范围；若不存在，请说明理由．
（1）4，（，）；（2）（0，1）；（3）1＜m＜2．
【解析】
试题分析：（1）当y=0时，即﹣x2+3x+4=0，解得：x1=4，x2=﹣1，∴点A（﹣1，0）点B（4，0），∴OB=4，y=﹣x2+3x+4=，∴抛物线的顶点坐标为（，），故答案为：4，（，）．
（2）如图，连接CP，CP′，
n=4时，﹣m2+3m+4=4，解得：m1=3，m2=0（舍去），∴这时P点...