题目内容
广东特产专卖店销售龙眼干，其进价为每斤40元，按每斤60元出售，平均每天可售出100斤，后来经调查发现，单价每降低2元，则平均每天的销售量增加20斤．每斤降价多少元，每天销售额最大？
20元
【解析】
试题分析：根据题意可以列出销售额与销售单价之间的关系式，然后整理为顶点式，即可解答本题．
【解析】
设每斤降价x元，销售额为y元，
y=（60﹣x）（100+）=﹣10（x﹣25）2+12250，
∴当x＜25时，y随x的增大而增大，
∵60﹣40=20，
∴0≤x≤20，
∴当x=20时，y取得最大值，
即每斤降价20元时...
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为12米，现在O点为原点，OM所在直线为x轴建立直角坐标系（如图所示）．
（1）直接写出点M及抛物线顶点P的坐标；
（2）求出这条抛物线的函数解析式；
（3）施工队计划在隧道门口搭建一个矩形“脚手架”ABCD，使A、D点在抛物线上，B、C点在地面OM上．为了筹备材料，需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少？请你帮施工队计算一下．
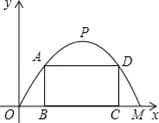
（1）M（12，0），P（6，6）；（2）y=x2+2x；（3）15米．
【解析】试题分析：确定了抛物线的顶点式，可以设抛物线的顶点式，又过原点（0，0），就可以确定抛物线解析式；设OB=x，由对称性得CM=x，这样就可以用含x的式子表示AB、AD、CD了，为求三根木杆AB、AD、DC的长度之和的最大值，提供依据．
试题解析：（1）M（12，0），P（6，6）
（2）∵顶点坐标（... 在Rt△ABC中，锐角∠A的平分线与锐角∠B的平分线相交于点D，则∠ADB＝______．
135°
【解析】在Rt△ABC中,∠CAB+∠CBA=180°?90°=90°，
∵锐角∠A的平分线与锐角∠B的平分线相交于点D，
∴∠DAB+∠DBA= (∠CAB+∠CBA)= ×90°=45°，
在△ABD中,∠ADB=180°?(∠DAB+∠DBA)=180°?45°=135°
故答案为：135°. 分解因式：16(x－y)2－9(x＋y)2.
(7x－y)(x－7y)
【解析】试题分析:利用平方差公式因式分解即可.
试题解析:
16(x－y)2－9(x＋y)2
=[4(x－y)－3(x＋y)][4(x－y)+3(x＋y)]
=(x－7y)(7x－y). 已知多项式x2＋a能用平方差公式在有理数范围内分解因式，那么在下列四个数中a可以等于( )
A. 9 B. 4
C. －1 D. －2
C
【解析】当x=-1时，x2-1=（x+1）（x-1），其它的三个选项都不符合要求，故选C. 将抛物线y=2（x﹣1）2+2向左平移3个单位，再向下平移4个单位，那么得到的抛物线的表达式为 ．
y=2﹣2
【解析】试题分析：按照“左加右减，上加下减”的规律可得抛物线y=2（x﹣1）2+2向左平移3个单位，再向下平移4个单位得到y=2（x﹣1+3）2+2﹣4=2（x+2）2﹣2．即可得抛物线的解析式为y=2（x+2）2﹣2． 二次函数y=a（x+m）2+n的图象如图，则一次函数y=mx+n的图象经过（ ）
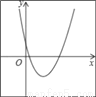
A. 第一、二、三象限 B. 第一、二、四象限
C. 第二、三、四象限 D. 第一、三、四象限
C
【解析】试题分析：根据抛物线的顶点在第四象限，得出n＜0，m＜0，即可得出一次函数y=mx+n的图象经过二、三、四象限．
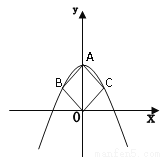
故选C． 如图在平面直角坐标系中，二次函数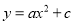
的图象过正方形ABOC的三个顶点A、B、C，则
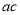值为__________。
-2
【解析】试题解析：设正方形的对角线OA长为2m，
则B（-m，m），C（m，m），A（0，2m）；
把A，C的坐标代入解析式可得：
c=2m①，am2+c=m②，
①代入②得：m2a+2m=m，解得：a=-，
则ac=-•2m=-2． 在等腰梯形ABCD中，AD∥BC，AE⊥BC于E，且AE=AD，BC＝3AE， 则∠BAD等于 （ ）
A. 120° B. 135° C. 130° D. 不能确定
B
【解析】【解析】
过点D作DF⊥BC于点F．
∵AE⊥BC，DF⊥BC，AD=AE，∴四边形AEFD为正方形，∴AD=EF．
∵AD=AE，BC=3AD，∴BE=AE=EF=FC，∴∠B=45°，∴∠BAD=135°．
故选B．