题目内容
已知抛物线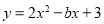
的对称轴是直线
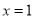，则
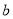的值为 ．
b=4
【解析】
试题分析：由抛物线的对称轴x=-和已知条件抛物线y=2-bx+3的对称轴是直线x=1，得到的等式，即可求出b的值．
快乐暑假暑假能力自测中西书局系列答案已知抛物线和直线l在同一直角坐标系中的图象如图所示，抛物线的对称轴为直线x=﹣1，P1（x1，y1）、P2（x2，y2）是抛物线上的点，P3（x3，y3）是直线l上的点，且﹣1＜x1＜x2，x3＜﹣1，则y1、y2、y3的大小关系为（ ）
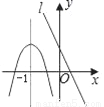
A. y1＜y2＜y3 B. y3＜y1＜y2 C. y3＜y2＜y1 D. y2＜y1＜y3
D
【解析】解析：对称轴为直线x=﹣1，且﹣1＜x1＜x2，当x＞﹣1时，y2＜y1，
又因为x3＜﹣1，由一次函数的图象可知，此时点P3（x3，y3）在二次函数图象上方，
所以y2＜y1＜y3．
故选：D． 已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=∠A，则此三角形（ ）
A. 一定有一个内角为45° B. 一定有一个内角为60°
C. 一定是直角三角形 D. 一定是钝角三角形
C
【解析】试题解析：∵∠A+∠B+∠C=180°，∠B+∠C=∠A，
∴2∠A=180°，
∴∠A=90°，
即△ABC一定是直角三角形；
故选C． 分解因式：16－x2＝( )
A. (4－x)(4＋x) B. (x－4)(x＋4)
C. (8＋x)(8－x) D. (4－x)2
A
【解析】试题分析：直接利用平方差公式分解因式得出答案．16﹣x2=（4﹣x）（4+x）． 已知函数y=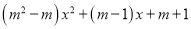
(1)若这个函数是一次函数，求m的值;
(2)若这个函数是二次函数，则m的值应怎样？
(1)、m=0；(2)、m≠0且m≠1.
【解析】试题分析：（1）由一次函数的定义求解；
（2）由二次函数的定义求解．
试题解析：（1）由一次函数的定义，得： ，解得m=0或m=1，又∵m﹣1≠0即m≠1；∴当m=0时，这个函数是一次函数；
（2）由二次函数的定义，得： ，解得且，∴当且时，这个函数是二次函数． 如图，小姚身高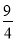
m在某次投篮中，球的运动路线是抛物线
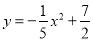的一部分，若命中篮圈中心，则他与篮底的距离
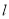是（ ）
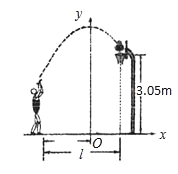
A. 3.5m B. 4m C. 4.5m D. 4.6m
B
【解析】试题分析：分别求出当y=3.05和当y=时的x的值，前面那个取正数，后面的那个取负数，然后计算它们之间的距离. 已知二次函数y=2x2+bx﹣1．
（1）求证：无论b取什么值，二次函数y=2x2+bx﹣1图象与x轴必有两个交点．
（2）若两点P（﹣3，m）和Q（1，m）在该函数图象上．
①求b、m的值；
②将二次函数图象向上平移多少单位长度后，得到的函数图象与x轴只有一个公共点？
（1）无论b取什么值，二次函数y=2x2+bx﹣1图象与x轴必有两个交点．
（2）b=4，m=5；（3）二次函数图象向上平移3个单位
【解析】
试题分析：（1）先计算判别式的值，再利用非负数的性质可判断△=＞0，然后根据判别式的意义可判断抛物线与x轴必有两个交点；
（2）①先利用抛物线的对称性可确定抛物线的对称轴方程，从而可求出b的值，然后计算自变量为1所对应的函数值即可得... 已知抛物线和直线l在同一直角坐标系中的图象如图所示，抛物线的对称轴为直线x=﹣1，P1（x1，y1），P2（x2，y2）是抛物线上的点，P3（x3，y3）是直线l上的点，且x3＜﹣1＜x1＜x2，则y1，y2，y3的大小关系是（ ）
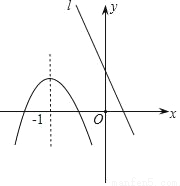
A. y1＜y2＜y3 B. y2＜y3＜y1 C. y3＜y1＜y2 D. y2＜y1＜y3
D
【解析】因为抛物线的对称轴为直线x=-1，开口向下，P1（x1，y1），P2（x2，y2）是抛物线上的点，且-1＜x1＜x2，根据二次函数的性质：在对称轴的右侧，y随x的增大而减小，可得y2＜ y1；P3（x3，y3）是直线l上的点，直线y随x的增大而减小，且x3＜-1，由图象可知，直线上x3对应的函数值y3大于-1对应的函数值，又因x=-1时，抛物线的顶点最高，可得y3最大，所以y2＜... 在□ABCD中，∠A∶∠B∶∠C∶∠D的值可以是（ ）
A.1∶2∶3∶4 B.1∶2∶2∶1
C.1∶1∶2∶2 D.2∶1∶2∶1
D．
【解析】
试题解析：∵四边形ABCD是平行四边形，
∴∠A=∠C，∠B=∠D，AB∥CD，
∴∠B+∠C=180°，∠A+∠D=180°，
即∠A和∠C的数相等，∠B和∠D的数相等，且∠B+∠C=∠A+∠D，
故选D．