嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图1的四边形ABCD，并写出了如下不完整的已知和求证．
已知：如图1，在四边形ABCD中，BC=AD，AB=
求证：四边形ABCD是 四边形．
（1）在方框中填空，以补全已知和求证；
（2）按嘉淇同学的思路写出证明过程；
（3）用文字叙述所证命题的逆命题.
（1）见解析；（2）见解析
【解析】试题分析：（1）命题的题设为“两组对边分别相等的四边形”，结论是“是平行四边形”，即可得到结论；
（2）连接BD，利用SSS定理证明△ABD≌△CDB可得∠ADB=∠DBC，∠ABD=∠CDB，进而可得AB∥CD，AD∥CB，根据两组对边分别平行的四边形是平行四边形可得四边形ABCD是平行四边形；
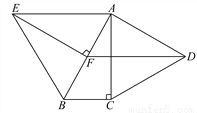
（3）把命题“两组对边分别相等的四边形是平行四... 如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD，等边△ABE.已知∠BAC＝30°，EF⊥AB，垂足为点F，连接DF.
(1)试说明AC＝EF；
(2)求证：四边形ADFE是平行四边形．
（1）证明见解析（2）证明见解析
【解析】证明：（1）∵△ABE是等边三角形，EF⊥AB，
∴∠AEF =∠AEB= 30º，AE=AB，∠EFA= 90º．
∵∠ACB= 90º，∠BAC= 30º，
∴∠EFA=∠ACB，∠AEF=∠BAC．
∴△AEF≌△BAC．
∴AC = EF．
（2）∵△ACD是等边三角形，
∴AC = AD，∠DAC=... 已知：如图，在正方形ABCD中，G是CD上一点，延长BC到E，使CE=CG，连接BG并延长交DE于F．
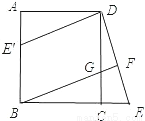
（1）求证：△BCG≌△DCE；
（2）将△DCE绕点D顺时针旋转90°得到△DAE′，判断四边形E′BGD是什么特殊四边形，并说明理由。
（1）答案见解析；（2）答案见解析
【解析】试题分析：（1）由正方形ABCD，得BC=CD，∠BCD=∠DCE=90°，又CG=CE，所以△BCG≌△DCE（SAS）．
（2）由（1）得BG=DE，又由旋转的性质知AE′=CE=CG，所以BE′=DG，从而证得四边形E′BGD为平行四边形．
（1）证明：∵四边形ABCD是正方形，
∴BC=CD，∠BCD=90°．
∵∠... 我们给出如下定义：若一个四边形的两条对角线相等，则称这个四边形为等对角线四边形．请解答下列问题：
（1）写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称；
（2）探究：当等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和与其中一条对角线的大小关系，并证明你的结论．
（1）梯形、矩形、正方形；（2）答案见解析
【解析】试题分析：（1）等腰梯形、矩形、正方形，任选两个即可；
（2）等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和大于或等于一条对角线的长．分两种情况证明：当BC与CE不在同一条直线上时，60°角所对的两边之和大于其中一条对角线的长；当BC与CE在同一条直线上时60°角所对的两边之和等于其中一条对角线的长．
... 如图，已知△ABC是等边三角形，D、E分别在边BC、AC上，且CD=CE，连接DE并延长至点F，使EF=AE，连接AF、BE和CF．
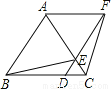
（1）请在图中找出一对全等三角形，用符号“≌”表示，并加以证明；
（2）判断四边形ABDF是怎样的四边形，并说明理由；
（3）若AB=6，BD=2DC，求四边形ABEF的面积．.
（1）见解析；（2）平行四边形；（3）
【解析】试题分析：（1）从图上及已知条件容易看出△BDE≌△FEC，△BCE≌△FDC，△ABE≌△ACF．判定两个三角形全等时，必须有边的参与，所以此题的关键是找出相等的边．
（2）由（1）的结论容易证明AB∥DF，BD∥AF，两组对边分别平行的四边形是平行四边形．
（3）EF∥AB，EF≠AB，四边形ABEF是梯形，只要求出此梯形的面积... 下列说法正确的是( )
A. 两个全等的三角形一定关于某条直线对称 B. 关于某条直线的对称的两个三角形一定全等
C. 直角三角形是轴对称图形 D. 锐角三角形都是轴对称图形
B
【解析】A.根据轴对称的定义，全等三角形不一定关于某直线对称，故错误；
B. 根据轴对称的性质,关于某条直线的对称的两个三角形一定全等,故正确;
C.直角三角形中，等腰直角三角形是轴对称图形，其它一般的直角三角形不是，故错误；
D.锐角三角形不一定是轴对称图形，如三个角分别是50°、60°、70°的三角形就不是轴对称图形，故错误.
故选B. 下列说法中正确的有( )
①角的两边关于角平分线对称; ②两点关于连结它的线段的中垂线对称
③成轴对称的两个三角形的对应点,或对应线段,或对应角也分别成轴对称
④到直线l距离相等的点关于l对称
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】①∵应该为角的两边关于“角平分线所在直线”对称,故不正确;
②“两点关于连结它的线段的中垂线对称”正确；
③“成轴对称的两个三角形的对应点,或对应线段,或对应角也分别成轴对称”正确；
④∵到直线l距离相等的点可以在l的同一侧,故不正确；
∴②和③正确.
故选B. 下列说法错误的是( )
A. 等边三角形是轴对称图形
B. 轴对称图形的对应边相等,对应角相等
C. 成轴对称的两条线段必在对称轴一侧
D. 成轴对称的两个图形对应点的连线被对称轴垂直平分
C
【解析】A. 由等边三角形的性质知,等边三角形是轴对称图形,正确;
B. 由轴对称的性质知,轴对称图形的对应边相等,对应角相等,正确;
C. 成轴对称的两条线段必在对称轴两侧,故错误;
D. 由轴对称的性质知,成轴对称的两个图形对应点的连线被对称轴垂直平分,正确;
故选C. 观察下列平面图形：其中属于轴对称图形的有( )
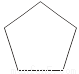
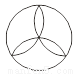
A. 1个 B. 2个 C. 3个 D. 4个
C
【解析】根据轴对称图形的定义可知，前三个图形分别有5条、5条、3条对称轴，最后一个图形三角形内的图案没有对称轴.
故选C. 如图所示，在桌面上坚直放置两块镜面相对的平面镜，在两镜之间放一个小凳，那么在两镜中共可得到小凳的像( )
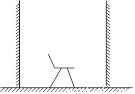
A. 2个 B. 4个 C. 16个 D. 无数个
D
【解析】∵两块镜面相对，
∴在每一块镜面中，都能有对方镜面的图像，
∴小凳在每一个镜面中都有图像.
∵每一个面中的小凳都在对面镜子中有图像，
∴循环往复，图像无数.
故选D