题目内容
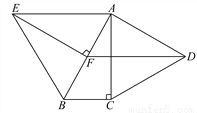
如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD，等边△ABE.已知∠BAC＝30°，EF⊥AB，垂足为点F，连接DF.
(1)试说明AC＝EF；
(2)求证：四边形ADFE是平行四边形．
（1）证明见解析（2）证明见解析
【解析】证明：（1）∵△ABE是等边三角形，EF⊥AB，
∴∠AEF =∠AEB= 30º，AE=AB，∠EFA= 90º．
∵∠ACB= 90º，∠BAC= 30º，
∴∠EFA=∠ACB，∠AEF=∠BAC．
∴△AEF≌△BAC．
∴AC = EF．
（2）∵△ACD是等边三角形，
∴AC = AD，∠DAC=...
练习册系列答案
阅读快车系列答案
相关题目
某班同学去春游花了250元包租了一辆客车，如果参加春游的同学每人交8元钱租车费，还不够，如果每人交9元，还用不了．用不等式表示出上述问题中存在的不等关系．
见解析
【解析】试题分析：根据每人交8元钱租车费，还不够可得8x＜250；根据如果每人交9元，还用不了可得9x＞250．
试题解析：设参加春游的同学x人，由题意得
. 两个图形关于某直线对称，对称点一定( )
A. 这直线的两旁 B. 这直线的同旁 C. 这直线上 D. 这直线两旁或这直线上
D
【解析】由成轴对称的定义知，成轴对称的两个图形的对称点，或者在对称轴上，或者在对称轴两旁.
故选D. 轴对称图形沿对称轴对折后，对称轴两旁的部分( )
A. 完全重合 B. 不完全重合 C. 两者都有 D. 不确定
A
【解析】由轴对称图形的定义知，轴对称图形沿对称轴对折后，对称轴两旁的部分完全重合.
故选A. 下列说法中正确的有( )
①角的两边关于角平分线对称; ②两点关于连结它的线段的中垂线对称
③成轴对称的两个三角形的对应点,或对应线段,或对应角也分别成轴对称
④到直线l距离相等的点关于l对称
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】①∵应该为角的两边关于“角平分线所在直线”对称,故不正确;
②“两点关于连结它的线段的中垂线对称”正确；
③“成轴对称的两个三角形的对应点,或对应线段,或对应角也分别成轴对称”正确；
④∵到直线l距离相等的点可以在l的同一侧,故不正确；
∴②和③正确.
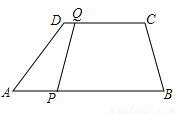
故选B. 如图，在梯形ABCD中，CD∥AB，且CD=6cm，AB=9cm，P、Q分别从A、C同时出发，P以1cm/s的速度由A向B运动，Q以2cm/s的速度由C向D运动．则________秒时，直线QP将四边形ABCD截出一个平行四边形
2或3
【解析】【解析】
设x秒时，直线QP将四边形ABCD截出一个平行四边形，则AP=xcm，BP=（9-x）cm，CQ=2xcm，DQ=（6-2x）cm．
∵CD∥AB，∴分两种情况：
1．当AP=DQ时，x=6-2x，解得：x=2；
2．当BP=CQ时，9-x=2x，解得：x=3；
综上所述：当2秒或3秒时，直线QP将四边形ABCD截出一个平行四边形．
... 下面几组条件中，能判断一个四边形是平行四边形的是（ ）
A．一组对边相等 B．两条对角线互相平分
C．一组对边平行 D．两条对角线互相垂直
B
【解析】
试题分析：平行四边形的五种判定方法分别是：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形；（4）两组对角分别相等的四边形是平行四边形；（5）对角线互相平分的四边形是平行四边形．根据平行四边形的判定方法，采用排除法，逐项分析判断．
【解析】
A、一组对边相等，不能判断，故错误；
... 下列说法正确的是( )
A. 可能性很小的事件在一次试验中一定不会发生
B. 可能性很小的事件在一次试验中一定发生
C. 可能性很小的事件在一次试验中有可能发生
D. 不可能事件在一次试验中也可能发生
C
【解析】试题分析：在随机试验中，可能出现也可能不出现，而在大量重复试验中具有某种规律性的事件叫做随机事件；不可能事件是指在大量重复实验中完全不会发生的事件.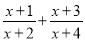 
的和是________
【解析】试题分析：
＝
＝
＝．
故答案为： ．