题目内容
下列说法中正确的有( )
①角的两边关于角平分线对称; ②两点关于连结它的线段的中垂线对称
③成轴对称的两个三角形的对应点,或对应线段,或对应角也分别成轴对称
④到直线l距离相等的点关于l对称
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】①∵应该为角的两边关于“角平分线所在直线”对称,故不正确;
②“两点关于连结它的线段的中垂线对称”正确；
③“成轴对称的两个三角形的对应点,或对应线段,或对应角也分别成轴对称”正确；
④∵到直线l距离相等的点可以在l的同一侧,故不正确；
∴②和③正确.
故选B.
练习册系列答案
相关题目
如图，在△ABC中，D、E分别是边AB、AC的中点，BC=8，则DE= ．
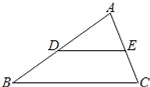
4
【解析】试题分析：已知D、E分别是边AB、AC的中点，BC=8，根据三角形的中位线定理得到DE=BC=4． 下列右侧四幅图中，平行移动到位置M后能与N成轴对称的是（ ）
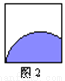
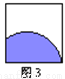
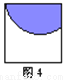
A. 图1 B. 图2 C. 图3 D. 图4
C
【解析】根据平移的性质即可解答.
解答：要想平行移动到位置M后能与N成轴对称，则一定是以M、N的公共边所在直线为对称轴，故选C. △ABC中，AB＝AC，点D与顶点A在直线BC同侧，且BD＝AD．则BD与CD的大小关系为( )
A. BD＞CD B. BD＝CD C. BD＜CD D. BD与CD大小关系无法确定
D
【解析】如下图，应该有三种情况：(1) BD＞CD，(2) BD＝CD ，3) BD＜CD.
故选D 以下结论正确的是( )．
A. 两个全等的图形一定成轴对称 B. 两个全等的图形一定是轴对称图形
C. 两个成轴对称的图形一定全等 D. 两个成轴对称的图形一定不全等
C
【解析】A中说法错误，应该是轴对称的两个图形一定全等，反过来不对，故不正确；
B中前后矛盾，两个全等的图形，是指两个图形，而后面的轴对称图形是指一个图形，故不正确；
C中根据轴对称的性质可以知道，成轴对称的两个图形，一定全等，故正确；
D中根据轴对称的性质可以知道，成轴对称的两个图形，一定全等，故不正确；
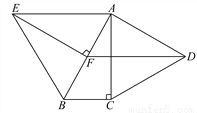
故选C. 如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD，等边△ABE.已知∠BAC＝30°，EF⊥AB，垂足为点F，连接DF.
(1)试说明AC＝EF；
(2)求证：四边形ADFE是平行四边形．
（1）证明见解析（2）证明见解析
【解析】证明：（1）∵△ABE是等边三角形，EF⊥AB，
∴∠AEF =∠AEB= 30º，AE=AB，∠EFA= 90º．
∵∠ACB= 90º，∠BAC= 30º，
∴∠EFA=∠ACB，∠AEF=∠BAC．
∴△AEF≌△BAC．
∴AC = EF．
（2）∵△ACD是等边三角形，
∴AC = AD，∠DAC=... 如图，在平面直角坐标系中，以O（0，0）、A（1，-1）、B（2，0）为顶点，构造平行四边形，下列各点中不能作为平行四边形第四个顶点坐标的是（ ）
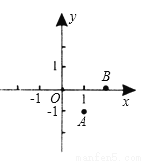
A. （3，-1） B. （-1，-1） C. （1，1） D. （-2，-1）
D
【解析】A、∵以O（0，0）、A（1，-1）、B（2，0）为顶点，构造平行四边形，
当第四个点为（3，-1）时，
∴BO=AC1=2，
∵A，C1，两点纵坐标相等，
∴BO∥AC1，
∴四边形OAC1B是平行四边形；故此选项正确；
B、∵以O（0，0）、A（1，-1）、B（2，0）为顶点，构造平行四边形，
当第四个点为（-1，-1）时，
∴... 一个不透明的口袋里装有5个红球,3个白球,2个绿球,这些球形状和大小完全相同,小明从中任意摸出一个球.
(1)你认为小明摸到的球很可能是什么颜色?为什么?
(2)摸到三种颜色球的可能性一样吗?
(3)如果想让小明摸到红色球和白色球的可能性一样,该怎么办?写出你的方案.
(1)红色，理由见解析；(2)不一样；(3)取2个红球出来,或放2个白球进去.
【解析】试题分析：（1）哪种球的数量多摸到哪种球的可能性就大；（2）根据球的数量多少判断；（3）让红球和白球的数量一样多即可.
【解析】
（1）小明很可能摸到红球，因为红球的数目多；
（2）可能性不一样，摸到红球的可能性最大，白色球次之，绿色球最小；
（3）答案不唯一，如把1号球先取出来，再进... 计算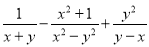
【解析】试题分析：把y－x转化为－(x－y)，x2－y2＝(x＋y)(x－y)，最简公分母为x2－y2，通分后再相加减即可．
试题解析：
【解析】
原式＝
＝
＝．