在直线、线段、角、两条平行直线组成的图形、两条相交直线组成的图形这些图形中，是轴对称图形的有( )
A. 5个 B. 4个 C. 3个 D. 2个
A
【解析】利用轴对称图形的定义对各图形进行判断即可得出结论.
【解析】
由轴对称的性质得，直线是轴对称图形，线段是有两条对称轴的轴对称图形，角的对称轴是其角平分线所在的直线；两条平行直线也是轴对称图形，两条相交直线也是轴对称图形，都是轴对称图形，故有5个.
故选A. 如图，△ABC和△A′B′C′关于直线l对称，下列结论中：
①△ABC≌△A′B′C′；
②∠BAC′=∠B′AC；
③l垂直平分CC′；
④直线BC和B′C′的交点不一定在l上，
正确的有（ ）
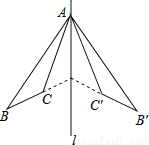
A. 4个 B. 3个 C. 2个 D. 1个
B
【解析】【解析】
∵△ABC和△A′B′C′关于直线l对称，
∴①△ABC≌△A′B′C′，正确；
②∠BAC=∠B′AC′，
∴∠BAC+∠CAC′=∠B′AC′+∠CAC′，
即∠BAC′=∠B′AC正确；
③l垂直平分CC′，正确；
④应为：直线BC和B′C′的交点一定在l上，故本小题错误．
综上所述，结论正确的是①②③共3个．
故... 如图，△ABC与△A′B′C′关于直线MN对称，P为MN上任一点，下列结论中错误的是（ ）
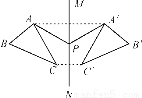
A. △AA′P是等腰三角形 B. MN垂直平分AA′，CC′
C. △ABC与△A′B′C′面积相等 D. 直线AB、A′B′的交点不一定在MN上
D
【解析】试题分析：△ABC与△A′B′C′关于直线MN对称，P为MN上任一点，所以根据轴对称图形的性质可以知道图形上对应点的连线被对称轴垂直且平分，所以△AA′P是等腰三角形；MN垂直平分AA′，CC′；△ABC与△A′B′C′面积相等；AA′若一个三角形是轴对称图形，则这个三角形一定是( ）
A. 等边三角形 B. 不等边三角形 C. 等腰三角形 D. 等腰直角三角形
C
【解析】根据轴对称图形的性质即可得出答案.
A等边三角形一定是轴对称图形，但轴对称三角形不一定是等边三角形；
B不等边三角形一定不是轴对称图形；
C等腰三角形一定是轴对称三角形；
D等腰直角三角形一定是轴对称图形，但是轴对称三角形不一定是等腰直角三角形.故选C. 下列说法正确的有( )个
①有一个外角是120°的等腰三角形是等边三角形．
②有两个外角相等的等腰三角形是等边三角形．
③有一边上的高也是这边上的中线的等腰三角形是等边三角形．
④三个外角都相等的三角形是等边三角形．
A. 4个 B. 3个 C. 2个 D. 1个
C
【解析】利用等腰三角形和等边三角形的性质及判定即可得出答案.
【解析】
①有一个外角是120°则其相邻的内角为60°，又是等腰三角形，所以必定是等边三角形，正确；
②有两个外角相等，则与这两个外角相邻的内角也相等，但是如果这两个内角就是原来等腰三角形的两个底角，则不能判定是等边三角形；故错误；
③有一边上的高也是这边上的中线，如果这条边恰好是原等腰三角形的底边，则不能... 如图,∠AOB内一点P,分别画出P关于OA、OB的对称点P1、P2连P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长为_______.
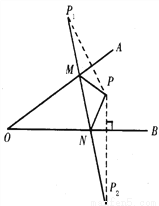
5cm
【解析】∵P、P1,P、P2关于OA、OB对称，
∴PM=P1M,PN=P2N，
∴△PMN的周长=P1P2，
∴△PMN的周长是5 cm. 如图，矩形ABCD中将其沿EF翻折后，D点恰落在B处，∠BFE= 650，则∠AEB=____________.
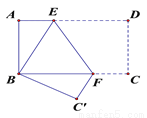
50°
【解析】根据翻折求出各个角的度数，再根据平角180°求出∠AEB的度数即可.
【解析】
如图所示，
由矩形ABCD可得AD∥BC，
∴∠1=∠BFE =65°，
由翻折得∠2=∠1 =65°，
∴∠AEB =180°-∠1- ∠2 =180°-65°-65°=50°. 如图，△ABC中，∠ A=500，∠C=700，BD、BE三等分∠ABC，将△BCE沿BE对折，点C落在C’处，则∠1=_________；
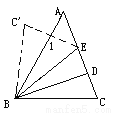
90°
【解析】根据翻折求出各个角的度数，再根据三角形的一个外角等于和它不相邻的两个内角的和求出∠1的度数.
【解析】
∵∠ A=500，∠C=700，
∴∠ABC =60°，
∵BD、BE三等分∠ABC，
∴∠ABE =∠EBD =∠DBC =20°，
∴∠EBC =∠EBD +∠DBC =40°，
由翻折得∠C’BE=∠EBC =40°， ∠C’ =... 如图，△ABE和△ADC是△ABC分别沿AB、AC边翻折得到的，若∠1: ∠2:∠3 = 28 :5 : 3， 则∠4的度数为__________
80°
【解析】根据翻折求出各个角的度数，再根据三角形的一个外角等于和它不相邻的两个内角的和求出∠4的度数.
【解析】
∵∠1: ∠2:∠3 = 28 :5 : 3，
∠1+∠2+∠3 = 180°，
∴∠1=140°，∠2=25°，∠3=15°，
由翻折得∠EBA =∠2 =25°，∠DCA =∠3 =15°，
∴∠EBC=∠EBA +∠2 =50°，∠DC... 如图△ABC中，AB=BC，∠A=36°，BD平分∠ABC交AC于D，则图中的等腰三角形有_____个
3
【解析】根据条件求出各个角的度数，由此确定哪个三角形是等腰三角形
解答：∵在△ABC中，AB=BC，∠A=36°，
∴∠ABC=∠ACB =72°，
∵BD平分∠ABC，
∴∠ABD=∠CBD =36°，
∴∠ABD=∠A =36°，∠BDC =72°=∠C，
∴△ABD和△BDC都是等腰三角形.
故有三个等腰三角形 故有三个.