题目内容
在直线、线段、角、两条平行直线组成的图形、两条相交直线组成的图形这些图形中，是轴对称图形的有( )
A. 5个 B. 4个 C. 3个 D. 2个
A
【解析】利用轴对称图形的定义对各图形进行判断即可得出结论.
【解析】
由轴对称的性质得，直线是轴对称图形，线段是有两条对称轴的轴对称图形，角的对称轴是其角平分线所在的直线；两条平行直线也是轴对称图形，两条相交直线也是轴对称图形，都是轴对称图形，故有5个.
故选A.
练习册系列答案
相关题目
已知一个多边形的内角和比它的外角和的3倍少180°，求这个多边形的边数．
7
【解析】试题分析：多边形的外角和是360°，根据多边形的内角和比它的外角和的3倍少180°，即可得到多边形的内角和的度数．根据多边形的内角和定理即可求得多边形的边数
试题解析：【解析】
设多边形的边数为n，依题意得
（n－2）．180°＝ 3×360°－180°
解得n＝7
答：这个多边形的边数是7 请你应用轴对称的知识画出图中的图形，并涂上彩色，与同学比一比，看谁画得正确、漂亮.
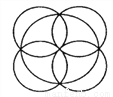
见解析
【解析】根据轴对称的知识进行图形设计即可.
【解析】
如图所示：
1.作一个正方形ABCD；
2.分别以正方形ABCD的四条边为直径，作四个圆；
3.以这四个圆的公共点为圆心O，OA长为半径作一个圆.
4.将线段与字母去掉.
就得到图中第二个图形.
然后按轴对称的要求涂色. 如图,∠AOB内一点P,分别画出P关于OA、OB的对称点P1、P2连P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长为_______.
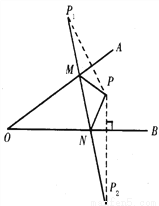
5cm
【解析】∵P、P1,P、P2关于OA、OB对称，
∴PM=P1M,PN=P2N，
∴△PMN的周长=P1P2，
∴△PMN的周长是5 cm. 下列右侧四幅图中，平行移动到位置M后能与N成轴对称的是（ ）
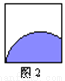
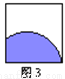
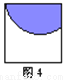
A. 图1 B. 图2 C. 图3 D. 图4
C
【解析】根据平移的性质即可解答.
解答：要想平行移动到位置M后能与N成轴对称，则一定是以M、N的公共边所在直线为对称轴，故选C. 下列各图都是一个汉字的一半,你能想像出它的另一半并能确定它是什么字吗?(有几个字的笔划在对称轴上)
，
，
，
，
.
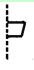见解析
【解析】试题分析：根据汉字的对称结构来确定是哪个汉字，对于第一个图，思考可能是口或中，但是口没有那么扁平，故为中；第二个图左边应该也是一个木，这样原来的汉字应该是林；第三个图形，根据轴对称可以容易得到是一个南字；第四个从对称上来研究，应该左边下方也有一个点，再考虑对称轴上可能有笔画，容易得到是京字；第五个图，从对称可以得到右边有点、横、捺，可是不是我们所学过的汉字，再考虑对称轴上的笔... 以下结论正确的是( )．
A. 两个全等的图形一定成轴对称 B. 两个全等的图形一定是轴对称图形
C. 两个成轴对称的图形一定全等 D. 两个成轴对称的图形一定不全等
C
【解析】A中说法错误，应该是轴对称的两个图形一定全等，反过来不对，故不正确；
B中前后矛盾，两个全等的图形，是指两个图形，而后面的轴对称图形是指一个图形，故不正确；
C中根据轴对称的性质可以知道，成轴对称的两个图形，一定全等，故正确；
D中根据轴对称的性质可以知道，成轴对称的两个图形，一定全等，故不正确；
故选C. 下列说法正确的是( )
A. 为了审核书稿中的错别字,选择抽样调查
B. 为了了解春节联欢晚会的收视率,选择全面调查
C. “射击运动员射击一次,命中靶心”是随机事件
D. “经过有交通信号灯的路口,遇到红灯”是必然事件
C
【解析】试题分析：为了审核书稿中的错别字，应选择全面调查，A错误；
为了了解春节联欢晚会的收视率，选择抽样调查，B错误；
“射击运动员射击一次，命中靶心”是随机事件，C正确；
“经过由交通信号灯的路口，遇到红灯”是随机事件，D错误．
故选C．