题目内容
如图，△ABC与△A′B′C′关于直线MN对称，P为MN上任一点，下列结论中错误的是（ ）
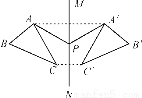
A. △AA′P是等腰三角形 B. MN垂直平分AA′，CC′
C. △ABC与△A′B′C′面积相等 D. 直线AB、A′B′的交点不一定在MN上
D
【解析】试题分析：△ABC与△A′B′C′关于直线MN对称，P为MN上任一点，所以根据轴对称图形的性质可以知道图形上对应点的连线被对称轴垂直且平分，所以△AA′P是等腰三角形；MN垂直平分AA′，CC′；△ABC与△A′B′C′面积相等；AA′
练习册系列答案
口算题天天练系列答案
相关题目
若x＞y，则下列式子中错误的是( )
A. x－3＞y－3 B. x＋3＞y＋3
C. －3x＞－3y D.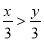 
C
【解析】试题分析：A、不等式的两边都减3，不等号的方向不变，故A正确；
B、不等式的两边都加3，不等号方向不变，故B正确；
C、不等式的两边都乘-3，不等号的方向改变，故C错误；
D、不等式的两边都除以3，不等号的方向改变，故D正确；
故选C． 某班同学去春游花了250元包租了一辆客车，如果参加春游的同学每人交8元钱租车费，还不够，如果每人交9元，还用不了．用不等式表示出上述问题中存在的不等关系．
见解析
【解析】试题分析：根据每人交8元钱租车费，还不够可得8x＜250；根据如果每人交9元，还用不了可得9x＞250．
试题解析：设参加春游的同学x人，由题意得
. 如图，两条相交直线l1与l2的夹角是45°，都是一个图案的对称轴，画出这个图案的其余部分．这个图案共有多少条对称轴？
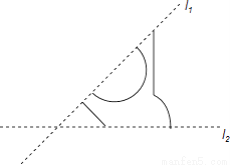
答案见解析.
【解析】试题分析：根据轴对称图形和对称轴的定义即可得到结果.
如图所示：
这个图案共有四条对称轴. 如图，△ABC中，∠ A=500，∠C=700，BD、BE三等分∠ABC，将△BCE沿BE对折，点C落在C’处，则∠1=_________；
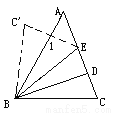
90°
【解析】根据翻折求出各个角的度数，再根据三角形的一个外角等于和它不相邻的两个内角的和求出∠1的度数.
【解析】
∵∠ A=500，∠C=700，
∴∠ABC =60°，
∵BD、BE三等分∠ABC，
∴∠ABE =∠EBD =∠DBC =20°，
∴∠EBC =∠EBD +∠DBC =40°，
由翻折得∠C’BE=∠EBC =40°， ∠C’ =... 桌面上有A、B两球，若要将B球射向桌面任意一边，使一次反弹后击中A，则如图所示8个点中，可以瞄准的点的个数（ ）
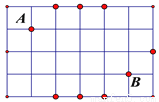
A. 1 B. 2 C. 4 D. 6
B
【解析】利用轴对称的性质准确画出图形即可得出答案.
【解析】
要想一次反弹后击中A，需要入射角也反射角相等，因此，可以经过如下图所示的两条路径达到要求，即B-D-A或者B-C-A，另外的一次反弹路线，都不经过图中给出的点，故选B. 两个图形关于某直线对称，对称点一定( )
A. 这直线的两旁 B. 这直线的同旁 C. 这直线上 D. 这直线两旁或这直线上
D
【解析】由成轴对称的定义知，成轴对称的两个图形的对称点，或者在对称轴上，或者在对称轴两旁.
故选D. 轴对称图形沿对称轴对折后，对称轴两旁的部分( )
A. 完全重合 B. 不完全重合 C. 两者都有 D. 不确定
A
【解析】由轴对称图形的定义知，轴对称图形沿对称轴对折后，对称轴两旁的部分完全重合.
故选A. 下列说法正确的是( )
A. 可能性很小的事件在一次试验中一定不会发生
B. 可能性很小的事件在一次试验中一定发生
C. 可能性很小的事件在一次试验中有可能发生
D. 不可能事件在一次试验中也可能发生
C
【解析】试题分析：在随机试验中，可能出现也可能不出现，而在大量重复试验中具有某种规律性的事件叫做随机事件；不可能事件是指在大量重复实验中完全不会发生的事件.