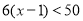题目内容
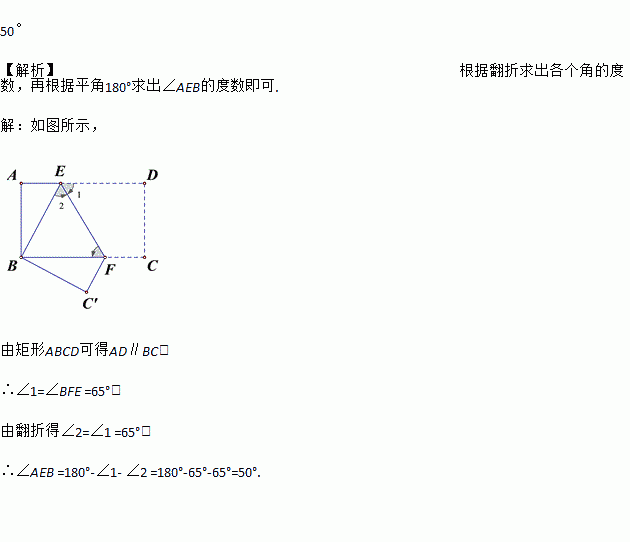
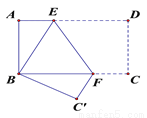
如图，矩形ABCD中将其沿EF翻折后，D点恰落在B处，∠BFE= 650，则∠AEB=____________.
50°
【解析】根据翻折求出各个角的度数，再根据平角180°求出∠AEB的度数即可.
【解析】
如图所示，
由矩形ABCD可得AD∥BC，
∴∠1=∠BFE =65°，
由翻折得∠2=∠1 =65°，
∴∠AEB =180°-∠1- ∠2 =180°-65°-65°=50°.
用不等号填空：(1)若a＞b，则ac2___bc2；(2)若a＞b，则3－2a___3－2b.
≥ <
【解析】（1）当c=0时，ac2=bc2，
当c≠0时， ac2＞bc2，
故答案为：≥；
（2）因为a>b，由不等式的性质3有：－2a<－2b，再由不等式的性质1得，3－2a＞3－2b，故答案为：<. 班级50名学生上体育课，老师出了一道题目：现在我拿来一些篮球，如果每5人一组玩一个篮球，有些同学没有球玩；如果每6人一组玩一个篮球，就会有一组玩篮球的人数不足6个．你们知道有几个篮球吗？
甲同学说：如果有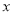
个篮球，
．
乙同学说：
．
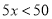丙同学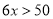说：
．
你明白他们的意思吗？
甲同学说的意思是：如果每5人一组玩一个篮球，那么玩球的人数少于50人，有些同学就没有球玩．
乙同学说的意思是：如果每6人一组玩一个篮球，那么就会有一个组玩篮球的人数不足6人．
丙同学说的意思是：如果每6人一组玩一个篮球，除了一个球以外，剩下的每6人玩一个球，还有几个（不足6人）玩另外一个篮球．
【解析】
试题分析：
甲同学说的意思是：如果每5人一组玩一个篮球，那么玩球... 下列不等关系一定正确的是（ ）
A.|a|＞0 B.﹣x2＜0 C.（x+1）2≥0 D.a2＞0
C
【解析】
试题分析：根据绝对值及完全平方式的性质求解．
【解析】
A、|a|≥0，错误；
B、﹣x2≤0，错误；
C、（x+1）2≥0，正确；
D、a2≥0，错误，
故选C． 用四块如图所示的两色正方形瓷砖，拼成一个新的正方形，使拼成轴对称图案，请至少给出三种不同的拼法：
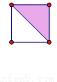
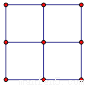
见解析
【解析】根据轴对称的概念进行图形设计即可.
【解析】
根据轴对称要求，设计出利用两色磁砖拼成的正方形如图所示. 如图，△ABC和△A′B′C′关于直线l对称，下列结论中：
①△ABC≌△A′B′C′；
②∠BAC′=∠B′AC；
③l垂直平分CC′；
④直线BC和B′C′的交点不一定在l上，
正确的有（ ）
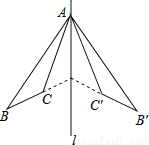
A. 4个 B. 3个 C. 2个 D. 1个
B
【解析】【解析】
∵△ABC和△A′B′C′关于直线l对称，
∴①△ABC≌△A′B′C′，正确；
②∠BAC=∠B′AC′，
∴∠BAC+∠CAC′=∠B′AC′+∠CAC′，
即∠BAC′=∠B′AC正确；
③l垂直平分CC′，正确；
④应为：直线BC和B′C′的交点一定在l上，故本小题错误．
综上所述，结论正确的是①②③共3个．
故... 如图，将一个等腰直角三角形按图示方式依次翻折，则下列说法正确的个数有（ ）
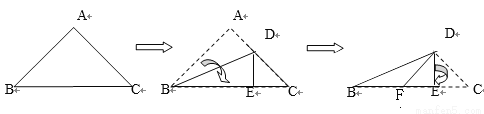
①DF平分∠BDE；②△BFD是等腰三角形；③△CED的周长等于BC的长
A. 1个 B. 2个 C. 3个 D. 0个
B
【解析】根据轴对称的性质即可得出答案.
【解析】
由多次翻折可得，∠DBE=∠ABD=∠ABC=×45°=22.5°，
∠CDE =90°－∠C =90°－45°=45°=∠C，
∠FDE=∠CDE =45°，
∴∠ABD=∠EDB=∠ADE=×(180°－∠CDE) =×(180°－45°)=67. 5°，
∴①DF平分∠BDE错误，如果正确的话，∠BD... 对于下列命题：（1）关于某一直线成轴对称的两个三角形全等；（2）等腰三角形的对称轴是顶角的平分线；（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点；（4）如果两个三角形全等，那么它们关于某直线成轴对称。其中真命题的个数为
A、0 B、1 C、2 D、3
C
【解析】
试题分析：根据平面图形的基本概念依次分析各小题即可作出判断.
（1）关于某一直线成轴对称的两个三角形全等，（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点，均为真命题；
（2）等腰三角形的对称轴是顶角的平分线所在的直线，（4）如果两个三角形全等，它们可能是平移或旋转构成的，均为假命题；
故选C. 把下列事件划分为两类,并说出划分标准.
①向空中抛一块石头,石头会飞向太空;
②甲、乙两名同学进行羽毛球比赛,甲获胜;
③从一副扑克牌中随意抽取一张牌,这张牌正好是红桃;
④黑暗中从一大串钥匙中随意选中一把,并用它打开了大门;
⑤两个负数的商小于0;
⑥在你们班中,任意选出一名同学,该同学是男生;
⑦明天的太阳从西方升起.
答案见解析
【解析】试题分析：按事件名称可将给出的几个事件划分为不可能事件和随机事件；然后按照事件发生的确定性，可将事件分为确定事件和不确定事件，据此进行分类即可.
解:按事件名称划分:不可能事件:①⑤⑦;随机事件:②③④⑥.