△ABC中，D、E分别为AB、AC的中点，若DE＝4，AD＝3，AE＝2，则△ABC的周长为______．
18
【解析】∵点D，E分别是△ABC的边AB，AC的中点，
∴DE是△ABC的中位线，
∴AB=2AD=2×3=6，AC=2AE＝2×2=4，BC=2DE=2×4=8，
∴AB+AC+BC=18，
即△ABC的周长为18，
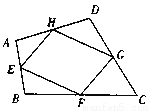
故答案为：18. 如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点，求证：四边形EFGH是平行四边形。
证明见解析
【解析】试题分析：连接AC，根据三角形的中位线的性质证得线段平行且相等，从而根据平行四边形的判定（一组对边平行且相等的四边形是平行四边形）得证.
试题解析：证明：连接AC
∵E，F，G，H是四边形ABCD的中点
∴EF，HG分别是△BCA和△DCA的中位线
∴EF∥AC，HG∥AC，且EF=
∴EF∥HG， EF=HG
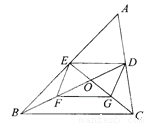
∴四边形EFGH是平行四... 已知：△ABC的中线BD、CE交于点O，F、G分别是OB、OC的中点．求证：四边形DEFG是平行四边形．
证明见解析.
【解析】试题分析：根据BD，CE是△ABC的中线可得DE是△ABC的中位线，F，G分别是OB，OC的中点可得FG是△BOC的中位线，根据三角形中位线定理可得DE∥BC且DE=BC，FG∥BC且FG=BC，进而可得DE∥FG且DE=FG，根据一组对边平行且相等的四边形是平行四边形可得结论.
试题解析：∵BD、CE是△ABC的中线，∴DE是△ABC的中位线，
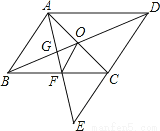
∴DE∥B... 已知：如图，E为□ABCD中DC边的延长线上的一点，且CE＝DC，连结AE分别交BC、BD于点F、G，连结AC交BD于O，连结OF．求证：AB＝2OF．
证明见解析.
【解析】
试题分析：先证明△ABF≌△ECF得BF=FC，再利用三角形中位线定理即可解决问题．
试题解析：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，AO=OC，
∵CD=CE，
∴AB=CE，∠BAF=∠CEF，
在△ABF和△ECF中，
，
∴△ABF≌△ECF，
∴BF=FC，
∵AO=OC，
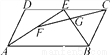
... 已知，如图，在?ABCD中，E是CD的中点，F是AE的中点，FC与BE交于点G.求证：GF＝GC.
证明见解析
【解析】试题分析：取BE的中点H，连接FH，CH，利用三角形中位线定理求FH＝AB,利用平行四边形判断定理可得到CEFH是平行四边形，所以GF＝GC.
试题解析：
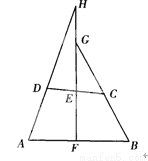
取BE的中点H，连接FH，CH，∵F是AE的中点，∴FH∥AB，FH＝AB.∵CD∥AB，CD＝AB，CE＝CD，∴CE∥FH，且CE＝FH.∴四边形CEFH是平行四边形．∴GF＝GC. 已知：如图，在四边形ABCD中，AD＝BC，E、F分别是DC、AB边的中点，FE的延长线分别与AD、BC的延长线交于H、G点．求证：∠AHF＝∠BGF．
证明见解析.
【解析】试题分析：连接AC，取AC中点为M，连接ME、MF，根据中位线定理证明EM=MF，从而可得∠MEF=∠MFE，根据平行线同位角相等，证明∠MEF=∠AHF，∠MFE=∠BGF，可以求证∠AHF=∠BGF．
试题解析：连接AC，取AC中点为M，连接ME、MF，如图：
∵E是CD的中点，M为AC中点，
∴EM∥AD，且EM=AD，
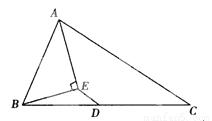
∵M是AC的中点，... 已知：如图，△ABC中，D是BC边的中点，AE平分∠BAC，BE⊥AE于E点，若AB＝5，AC＝7，求ED．
ED=1.
【解析】延长BE交AC于F，
∵AE平分∠BAC，
∴∠BAE＝∠CAE，
∵BE⊥AE，AE＝AE，
∴△ABE≌△AFE，
∴AF＝AB，BE＝EF，
∵AB＝5，
∴AF＝5，
∵AC＝7，
∴CF＝AC-AF＝7-5＝2，
∵D为BC中点，
∴BD＝CD，
∴DE是△BCF的中位线，
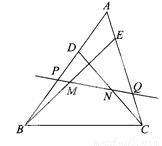
∴DE＝C... 如图在△ABC中，D、E分别为AB、AC上的点，且BD＝CE，M、N分别是BE、CD的中点．过MN的直线交AB于P，交AC于Q，线段AP、AQ相等吗?为什么?
AP=AQ，理由见解析.
【解析】根据中位线定理证明MH=NH，进而证明∠HMN=∠HNM，∠HMN=∠PQA，所以△APQ为等腰三角形，即AP=AQ． 过多边形的一个顶点的所有对角线把多边形分成8个三角形，这个多边形的边数是( )
A. 8 B. 9 C. 10 D. 11
C
【解析】设多边形有n条边，
则n-2=8，解得n=10，
所以这个多边形的边数是10，
故选C. 六边形的内角和是（ ）
A．540° B．720° C．900° D．360°
B．
【解析】
试题分析：根据多边形的内角和公式可得六边形的内角和是（6﹣2）×180°=720°，故答案选B．