题目内容
六边形的内角和是( )
A.540° B.720° C.900° D.360°
 B.
【解析】
试题分析:根据多边形的内角和公式可得六边形的内角和是(6﹣2)×180°=720°,故答案选B.
B.
【解析】
试题分析:根据多边形的内角和公式可得六边形的内角和是(6﹣2)×180°=720°,故答案选B.
练习册系列答案
相关题目
下列多项式能用完全平方公式分解因式的是( )
A. 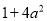 B.
B. 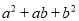 C.
C. 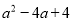 D.
D. 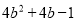
 C
【解析】根据完全平方公式: ,可以进行判断出答案是C选项正确.
故选:C.
C
【解析】根据完全平方公式: ,可以进行判断出答案是C选项正确.
故选:C. 化简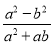 的结果为( )
的结果为( )
A. 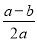 B.
B. 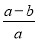 C.
C. 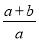 D.
D. 
 B
【解析】=,故选B.
B
【解析】=,故选B. 在五边形ABCDE中,∠A+∠B=240°,∠C=∠D=∠E=2∠B.求∠B的度数.
 50°
【解析】试题分析:首先求得五边形ABCDE的内角和,设∠B=x°,即可利用x表示其它角的度数,根据多边形的内角和定理即可列方程,从而求得∠B的度数.
试题解析:五边形ABCDE的内角和是(5-2)×180°=540°,
设∠B=x°,则∠C=∠D=∠E=2∠B=2x°,
∵∠A+∠B=240°
∴∠A=240-x°
∵∠A+∠B+∠C+∠D+∠E=540...
50°
【解析】试题分析:首先求得五边形ABCDE的内角和,设∠B=x°,即可利用x表示其它角的度数,根据多边形的内角和定理即可列方程,从而求得∠B的度数.
试题解析:五边形ABCDE的内角和是(5-2)×180°=540°,
设∠B=x°,则∠C=∠D=∠E=2∠B=2x°,
∵∠A+∠B=240°
∴∠A=240-x°
∵∠A+∠B+∠C+∠D+∠E=540... 若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A. 7 B. 10 C. 35 D. 70
 C
【解析】由正n边形的每个内角为144°结合多边形内角和公式,即可得出关于n的一元一次方程,解方程即可求出n的值,将其代入中即可得出结论.
【解析】
∵一个正n边形的每个内角为144°,
∴144n=180×(n﹣2),解得:n=10.
这个正n边形的所有对角线的条数是:==35.
故选C.
C
【解析】由正n边形的每个内角为144°结合多边形内角和公式,即可得出关于n的一元一次方程,解方程即可求出n的值,将其代入中即可得出结论.
【解析】
∵一个正n边形的每个内角为144°,
∴144n=180×(n﹣2),解得:n=10.
这个正n边形的所有对角线的条数是:==35.
故选C. 已知,如图,在?ABCD中,E是CD的中点,F是AE的中点,FC与BE交于点G.求证:GF=GC.
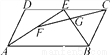
 证明见解析
【解析】试题分析:取BE的中点H,连接FH,CH,利用三角形中位线定理求FH=AB,利用平行四边形判断定理可得到CEFH是平行四边形,所以GF=GC.
试题解析:
取BE的中点H,连接FH,CH,∵F是AE的中点,∴FH∥AB,FH=AB.∵CD∥AB,CD=AB,CE=CD,∴CE∥FH,且CE=FH.∴四边形CEFH是平行四边形.∴GF=GC.
证明见解析
【解析】试题分析:取BE的中点H,连接FH,CH,利用三角形中位线定理求FH=AB,利用平行四边形判断定理可得到CEFH是平行四边形,所以GF=GC.
试题解析:
取BE的中点H,连接FH,CH,∵F是AE的中点,∴FH∥AB,FH=AB.∵CD∥AB,CD=AB,CE=CD,∴CE∥FH,且CE=FH.∴四边形CEFH是平行四边形.∴GF=GC. 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
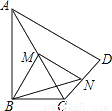
 (1)证明见解析;(2)
【解析】试题分析:(1)在△CAD中,由中位线定理得到MN∥AD,且MN=AD,在Rt△ABC中,因为M是AC的中点,故BM=AC,即可得到结论;
(2)由∠BAD=60°且AC平分∠BAD,得到∠BAC=∠DAC=30°,由(1)知,BM=AC=AM=MC,得到∠BMC =60°.由平行线性质得到∠NMC=∠DAC=30°,故∠BMN90°,得到,再由MN=...
(1)证明见解析;(2)
【解析】试题分析:(1)在△CAD中,由中位线定理得到MN∥AD,且MN=AD,在Rt△ABC中,因为M是AC的中点,故BM=AC,即可得到结论;
(2)由∠BAD=60°且AC平分∠BAD,得到∠BAC=∠DAC=30°,由(1)知,BM=AC=AM=MC,得到∠BMC =60°.由平行线性质得到∠NMC=∠DAC=30°,故∠BMN90°,得到,再由MN=... 有一个两位数,个位上的数字为a,十位上的数字为b,如果把这个两位数的个位与十位上的数字对调,得到的两位数大于原来的两位数,那么a与b哪个大?
 a>b
【解析】试题分析:根据题意得到不等式10b+a<10a+b,通过解该不等式即可比较它们的大小.
试题解析:根据题意,得
10b+a<10a+b,
所以,9b<9a,
所以,b<a,即a>b.
a>b
【解析】试题分析:根据题意得到不等式10b+a<10a+b,通过解该不等式即可比较它们的大小.
试题解析:根据题意,得
10b+a<10a+b,
所以,9b<9a,
所以,b<a,即a>b. 如图,A与A′关于直线MN对称,P是BA′与MN的交点.若P1为直线MN上任意一点(不与P重合),连结AP1、BP1,试说明 AP1+BP1>AP+BP.
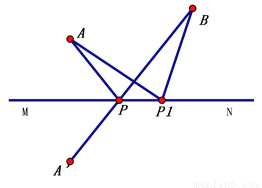
 见解析
【解析】试题分析:由三角形三条边的关系可得A′P1+BP1>A′B,再由轴对称的性质可得AP1=A′P1,然后通过等量代换可证明结论.
【解析】
如图,连结AP1,则在△A′P1B中,有A′P1+BP1>A′B
∴A′P1+BP1>A′P+PB
∵A与A′关于直线MN对称,
∴AP1与A′P1关于直线MN对称
∴AP1=A′P1
同理可得:AP=...
见解析
【解析】试题分析:由三角形三条边的关系可得A′P1+BP1>A′B,再由轴对称的性质可得AP1=A′P1,然后通过等量代换可证明结论.
【解析】
如图,连结AP1,则在△A′P1B中,有A′P1+BP1>A′B
∴A′P1+BP1>A′P+PB
∵A与A′关于直线MN对称,
∴AP1与A′P1关于直线MN对称
∴AP1=A′P1
同理可得:AP=... 
