题目内容
已知：如图，在四边形ABCD中，AD＝BC，E、F分别是DC、AB边的中点，FE的延长线分别与AD、BC的延长线交于H、G点．求证：∠AHF＝∠BGF．
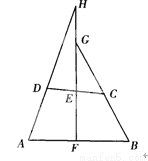
证明见解析.
【解析】试题分析：连接AC，取AC中点为M，连接ME、MF，根据中位线定理证明EM=MF，从而可得∠MEF=∠MFE，根据平行线同位角相等，证明∠MEF=∠AHF，∠MFE=∠BGF，可以求证∠AHF=∠BGF．
试题解析：连接AC，取AC中点为M，连接ME、MF，如图：
∵E是CD的中点，M为AC中点，
∴EM∥AD，且EM=AD，
∵M是AC的中点，...
练习册系列答案
教材全解字词句篇系列答案
相关题目
如图，△ABC和△DAE中，∠BAC=∠DAE，AB=AE，AC=AD，连接BD，CE，求证：△ABD≌△AEC．
证明见解析.
【解析】试题分析：观察图形，由∠BAC=∠DAE易证∠BAD=∠CAE，然后根据SAS证明三角形全等. 在代数式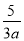
， 
， 
， 
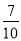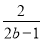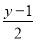，x+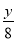
中，是分式的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】在代数式， ，， ，x+的分母中均不含有字母，因此它们是整式，而不是分式．
而,分母中含有字母，因此是分式．
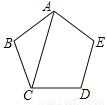
故选B. 如图，AC是正五边形ABCDE的一条对角线，则∠ACB= ．
36°．
【解析】
试题分析：∵五边形ABCDE是正五边形，∴∠B=108°，AB=CB，∴∠ACB=（180°﹣108°）÷2=36°；故答案为：36°． 若n边形内角和为900°，则边数n= ．
7．
【解析】
试题分析：根据题意得：180（n﹣2）=900，解得：n=7．故答案为：7． △ABC中，D、E分别为AB、AC的中点，若DE＝4，AD＝3，AE＝2，则△ABC的周长为______．
18
【解析】∵点D，E分别是△ABC的边AB，AC的中点，
∴DE是△ABC的中位线，
∴AB=2AD=2×3=6，AC=2AE＝2×2=4，BC=2DE=2×4=8，
∴AB+AC+BC=18，
即△ABC的周长为18，
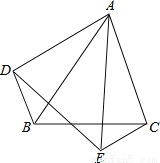
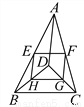
故答案为：18. 如图，D是△ABC内一点，BD⊥CD，AD＝6，BD＝4，CD＝3，E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是__.
11
【解析】试题解析：∵BD⊥DC，BD=4，CD=3，由勾股定理得，
∵E、F、G、H分别是AB、AC、CD、BD的中点，
∴HG=BC=EF，EH=FG=AD，
∵AD="6，"
∴EF="HG=2.5，EH=GF=3，"
∴四边形EFGH的周长是EF+FG+HG+EH=2×（2.5+3）=11． 有如图所示的两种广告牌，其中图（1）是由两个等腰直角三角形构成的，图（2）是一个矩形，从图形上确定这两个广告牌面积的大小关系，并将这种大小关系用含字母a，b的不等式表示为__________．
a2＋b2＞ab (a≠b)
【解析】试题分析：由图上可看出：图1可看做是长为a，宽为b的长方形加上一个小直角三角形；图2可看做是长为a，宽为b的长方形，根据不等关系：图1的面积＞图2的面积，即可列出不等式．
根据图形的面积公式，得图1的面积是a2＋b2，图2的面积是ab
再根据图形的面积大小关系，得a2＋b2＞ab（a≠b）. 找出图中是轴对称图形的图形,并找出两对对应点、两对对应线段、两对对应角.
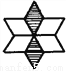
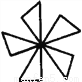
（1） (2) (3)
见解析
【解析】试题分析：本题考查了利用轴对称设计图案的知识,解答本题的关键是熟练掌握轴对称的性质.观察可知①是轴对称图形,先确定对称轴,然后找对应点、对应线段及对应角.
【解析】
第一个图形是轴对称图形，第二、三个图形是旋转对称图形.
如上图所示，若以EF为对称轴,则点A与点B、点M与点N、点C与点D等是对应点.线段AG与BH、CM与DN、PG与PH等是对应线段,∠A与∠B、...