题目内容
△ABC中，D、E分别为AB、AC的中点，若DE＝4，AD＝3，AE＝2，则△ABC的周长为______．
18
【解析】∵点D，E分别是△ABC的边AB，AC的中点，
∴DE是△ABC的中位线，
∴AB=2AD=2×3=6，AC=2AE＝2×2=4，BC=2DE=2×4=8，
∴AB+AC+BC=18，
即△ABC的周长为18，
故答案为：18.
练习册系列答案
阅读快车系列答案
相关题目
如图，MN与PQ相交于点O，MO=OP，QO=ON，∠M=65°，∠Q=30°，则∠P=____，∠N=___.
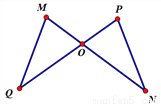
65° 30°
【解析】∵MO=OP，QO=ON（已知），
∠MO Q=∠PO N（对顶角相等）
∴△MOQ≌△PON（SAS）
∴∠P=∠M=65°，
∠N=∠Q=30°
故答案为：65°；30° 根据不等式的基本性质，可将“mx＜2”化为“x＞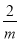
”，则m的取值范围是_____.
m＜0
【解析】因为mx＜2化为x＞，
根据不等式的基本性质3得：m＜0，
故答案为：m＜0． 设四边形的内角和等于a，五边形的外角和等于b，则a与b的关系是（ ）
A. a＞b B. a=b C. a＜b D. b=a+180°
B
【解析】∵四边形的内角和等于a，
∴a=（4﹣2）•180°=360°．
∵五边形的外角和等于b，
∴b=360°，
∴a=b．
故选B． 已知：如图，在四边形ABCD中，AD＝BC，E、F分别是DC、AB边的中点，FE的延长线分别与AD、BC的延长线交于H、G点．求证：∠AHF＝∠BGF．
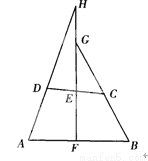
证明见解析.
【解析】试题分析：连接AC，取AC中点为M，连接ME、MF，根据中位线定理证明EM=MF，从而可得∠MEF=∠MFE，根据平行线同位角相等，证明∠MEF=∠AHF，∠MFE=∠BGF，可以求证∠AHF=∠BGF．
试题解析：连接AC，取AC中点为M，连接ME、MF，如图：
∵E是CD的中点，M为AC中点，
∴EM∥AD，且EM=AD，
∵M是AC的中点，... 如图，AC、BD是四边形ABCD的对角线，E、F分别是AD、BC的中点，M、N分别是BD、AC的中点．
求证：EF与MN互相平分．
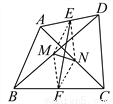
证明见解析.
【解析】试题分析：连接EM、EN、FM、FN，证明四边形EMFN为平行四边形，根据平行四边形对角线互相平分即可得.
试题解析：连接EM、EN、FM、FN，
∵E为AD的中点，N为AC的中点，
∴EN是△ACD的是位线，
∴EN∥CD，EN＝CD，
同理MF∥CD，MF＝CD，
∴EN∥MF，EN＝MF，
∴四边形EMFN为平行四边形，
... 如图，在△ABC中，∠ACB=90°，AC=8，AB="10." DE垂直平分AC交AB于点E，则DE的长为（ ）
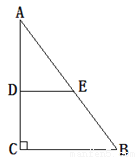
A. 6 B. 5 C. 4 D. 3
D
【解析】试题分析：已知，在△ABC中，∠ACB=90°，AC=8，AB=10，根据勾股定理可得BC=6，又因DE垂直平分AC，∠ACB=90°，可得DE为△ABC的中位线，根据三角形的中位线定理可得DE=BC=3，故答案选D. 用不等号连接下列各对数：（1）-
_______-
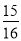，（2）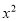 
+1 _______0 ．
> >
【解析】（1）∵， ，∴，
故答案为：>；
（2）∵x2≥0，∴x2+1>0，
故答案为：>. 设A、B两点关于直线MN轴对称,则_______垂直平分________.
直线MN 线段AB
【解析】∵A、B两点关于直线MN轴对称，
∴由轴对称的性质可得，直线MN垂直平分线段AB.