化简下列各分式.
(1)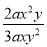 ; (2)
; (2)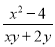 .
.
 (1) (2) .
【解析】(1) =;
(2)原式=.
故答案为:(1) (2) .
(1) (2) .
【解析】(1) =;
(2)原式=.
故答案为:(1) (2) . 不改变分式的值,使下列分式的分子和分母的最高次项的系数为正数.
(1)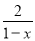 ; (2)
; (2)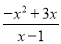 ; (3)
; (3)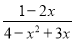 .
.
 (1)- . (2)- . (3)
【解析】根据分式的分子、分母及本身的符号,任意改变其中的两个,分式的值不变可得:(1) =- ;
(2) =
(3) =
(1)- . (2)- . (3)
【解析】根据分式的分子、分母及本身的符号,任意改变其中的两个,分式的值不变可得:(1) =- ;
(2) =
(3) = 先化简,后求值: 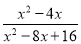 ,其中x=5.
,其中x=5.
 5
【解析】原式=,
把x=5代入得,原式=5.
5
【解析】原式=,
把x=5代入得,原式=5. 若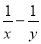 =3 ,求
=3 ,求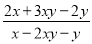 的值.
的值.
 【解析】分析:由已知可知x-y=-3xy,然后代入所求的式子,进行约分就可求出结果.
本题解析:
∵ =3,∴y-x=3xy, ∴x-y=-3xy,
∴ =.
【解析】分析:由已知可知x-y=-3xy,然后代入所求的式子,进行约分就可求出结果.
本题解析:
∵ =3,∴y-x=3xy, ∴x-y=-3xy,
∴ =. 已知x2+3x-1=0,求x-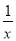 和x2+
和x2+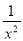 的值.
的值.
 -3,11
【解析】分析:首先将3x移项,再方程两边同除以x得出即可,再利用,方程两边同时平方求出即可.
本题解析:
因为 ,
所以 ,
将上式子两边同时除以x(x≠0),
所以 ,
,
,
则.故答案为:-3,,11.
-3,11
【解析】分析:首先将3x移项,再方程两边同除以x得出即可,再利用,方程两边同时平方求出即可.
本题解析:
因为 ,
所以 ,
将上式子两边同时除以x(x≠0),
所以 ,
,
,
则.故答案为:-3,,11. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
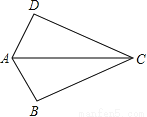
A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
 C
【解析】试题分析:本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能. A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC...
C
【解析】试题分析:本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能. A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC... 如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是( )
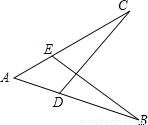
A. ∠B=∠C B. ∠AEB=∠ADC C. AE=AD D. BE=DC
 C
【解析】∵AB=AC (已知),∠A=∠A(公共角),
∴只需要AE=AD,
∴△ABE≌△ACD,
故选:C.
C
【解析】∵AB=AC (已知),∠A=∠A(公共角),
∴只需要AE=AD,
∴△ABE≌△ACD,
故选:C. 如图,已知E,F是AC上的两点,AE=CF,DF=BE,∠AFD=∠CEB,则下列不成立的是( )
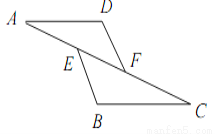
A. ∠A=∠C B. AD=CB C. BC=DF D. DF∥BE
 C
【解析】∵AE=CF(已知),
∴AE+EF=EF+CF,
∴AF=EC,
∵∠AFD=∠CEB,
∴△AFD≌△CEB(SAS),
∴∠A=∠C,
AD=CB,BC=DA,
∵∠AFD=∠CEB,
∴DF∥BE.
故选:C.
C
【解析】∵AE=CF(已知),
∴AE+EF=EF+CF,
∴AF=EC,
∵∠AFD=∠CEB,
∴△AFD≌△CEB(SAS),
∴∠A=∠C,
AD=CB,BC=DA,
∵∠AFD=∠CEB,
∴DF∥BE.
故选:C. 如图,在△ABD中,AC⊥BD,点C是BD的中点,则下列结论错误的是( )
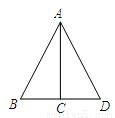
A. AB=AD B. AB=BD C. ∠B=∠D D. AC平分∠BAD
 B
【解析】∵AC⊥BD,点C是BD的中点,
∴AB=AD(线段中垂线的性质)
∴∠B=∠D(等边对等角)
∴∠BAC=∠DAC(等腰三角形三线合一)
∴AC平分∠BAD,
故选:B .
B
【解析】∵AC⊥BD,点C是BD的中点,
∴AB=AD(线段中垂线的性质)
∴∠B=∠D(等边对等角)
∴∠BAC=∠DAC(等腰三角形三线合一)
∴AC平分∠BAD,
故选:B . 如图,FE=BC,DE=AB,∠B=∠E=40°,∠F=70°,则∠A=( )
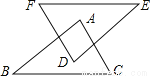
A. 40° B. 50° C. 60° D. 70°
 D
【解析】∵∠E=40°,∠F=70°,
∴∠D =70°,
∵FE=BC,DE=AB,∠B=∠E=40°,
∴△ABC≌△DEF(SAS)
∴∠A=∠D =70°.
故选:D .
D
【解析】∵∠E=40°,∠F=70°,
∴∠D =70°,
∵FE=BC,DE=AB,∠B=∠E=40°,
∴△ABC≌△DEF(SAS)
∴∠A=∠D =70°.
故选:D .