题目内容
如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是( )
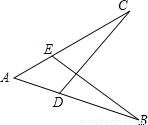
A. ∠B=∠C B. ∠AEB=∠ADC C. AE=AD D. BE=DC
 C
【解析】∵AB=AC (已知),∠A=∠A(公共角),
∴只需要AE=AD,
∴△ABE≌△ACD,
故选:C.
C
【解析】∵AB=AC (已知),∠A=∠A(公共角),
∴只需要AE=AD,
∴△ABE≌△ACD,
故选:C.
练习册系列答案
相关题目
用提公因式法分解多项式: 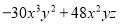
 【解析】试题分析:根据提公因式法--因式分解,确定公因式后提取公因式即可.
试题解析: .
【解析】试题分析:根据提公因式法--因式分解,确定公因式后提取公因式即可.
试题解析: . 下列能用平方差公式分解因式的是( )
A. 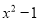 B.
B. 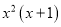 C.
C. 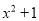 D.
D. 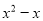
 A
【解析】根据平方差公式: ,A选项: ,可知能用平方差公式进行因式分解.
故选:A.
A
【解析】根据平方差公式: ,A选项: ,可知能用平方差公式进行因式分解.
故选:A. 如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形有( )
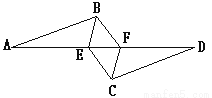
A. 1对 B. 2对 C. 3对 D. 4对
 C
【解析】∵AB∥CD,
∴∠A=∠D,
∵AB=CD,AE=FD,
∴△ABE≌△DCF(SAS),
∴BE=CF,∠BEA=∠CFD,
∴∠BEF=∠CFE,
∵EF=FE,
∴△BEF≌△CFE(SAS),
∴BF=CE,
∵AE=DF,
∴AE+EF=DF+EF,
即AF=DE,
∴△ABF≌△CDE(SSS)...
C
【解析】∵AB∥CD,
∴∠A=∠D,
∵AB=CD,AE=FD,
∴△ABE≌△DCF(SAS),
∴BE=CF,∠BEA=∠CFD,
∴∠BEF=∠CFE,
∵EF=FE,
∴△BEF≌△CFE(SAS),
∴BF=CE,
∵AE=DF,
∴AE+EF=DF+EF,
即AF=DE,
∴△ABF≌△CDE(SSS)... 在下列说法中,正确的有( )个.
①三角对应相等的两个三角形全等;②三边对应相等的两个三角形全等;③两角,一边对应相等的两个三角形全等;④两边,一角对应相等的两个三角形全等.
A. 1 B. 2 C. 3 D. 4
 B
【解析】①三角对应相等的两个三角形不一定全等,错误;
②三边对应相等的两个三角形全等,正确;
③两个角和其中一角的对边对应相等的两个三角形全等,正确;
④两条边和其中一边的对角对应相等的两个三角形不一定全等,错误;
故选:B
B
【解析】①三角对应相等的两个三角形不一定全等,错误;
②三边对应相等的两个三角形全等,正确;
③两个角和其中一角的对边对应相等的两个三角形全等,正确;
④两条边和其中一边的对角对应相等的两个三角形不一定全等,错误;
故选:B 不改变分式的值,使下列分式的分子和分母的最高次项的系数为正数.
(1)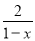 ; (2)
; (2)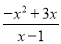 ; (3)
; (3)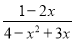 .
.
 (1)- . (2)- . (3)
【解析】根据分式的分子、分母及本身的符号,任意改变其中的两个,分式的值不变可得:(1) =- ;
(2) =
(3) =
(1)- . (2)- . (3)
【解析】根据分式的分子、分母及本身的符号,任意改变其中的两个,分式的值不变可得:(1) =- ;
(2) =
(3) = 化简分式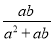 的结果为_____.
的结果为_____.
 【解析】= ,故答案为: .
【解析】= ,故答案为: . 把不等式2x>3-x化为x>a或x<a的形式是( )
A. x>3 B. x<3
C. x>1 D. x<1
 C
【解析】2x>3-x,
两边同时加上x,
2x+x>3,
3x>3,
两边同时除以3得
x>1,
故选C.
C
【解析】2x>3-x,
两边同时加上x,
2x+x>3,
3x>3,
两边同时除以3得
x>1,
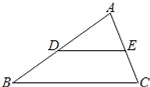
故选C. 如图,在△ABC中,D、E分别是边AB、AC的中点,BC=8,则DE= .
 4
【解析】试题分析:已知D、E分别是边AB、AC的中点,BC=8,根据三角形的中位线定理得到DE=BC=4.
4
【解析】试题分析:已知D、E分别是边AB、AC的中点,BC=8,根据三角形的中位线定理得到DE=BC=4. 
