下面命题不正确的是（ ）
A. 两个内角分别是50°和65°的三角形是等腰三角形
B. 两个外角相等的三角形是等腰三角形
C. 一个外角的平分线平行于一边的三角形是等腰三角形
D. 两个内角不相等的三角形不是等腰三角形
D
【解析】解：A．第三个角180°﹣50°﹣65°=65°，有两角相等的三角形是等腰三角形，正确；
B．外角相等，则对应的内角也相等，有两角相等的三角形是等腰三角形，正确；
C．利用两直线平行，内错角相等，同位相等，可知，另外的两内角也相等，有两角相等的三角形是等腰三角形，正确；
D．两个内角不相等的三角形可能是等腰三角形，错误．
故选D． 下列选项中，可以用来证明命题“若a2＞1，则a＞1”是假命题的反例是（ ）
A. a=﹣2 B. a=﹣1 C. a=1 D. a=2
A
【解析】试题分析：此题主要考查了利用举例法证明一个命题错误，要说明数学命题的错误，只需举出一个反例即可这是数学中常用的一种方法．根据要证明一个结论不成立，可以通过举反例的方法来证明一个命题是假命题．
用来证明命题“若a2＞1，则a＞1”是假命题的反例可以是：a=-2，
∵（-2）2＞1，但是a=-2＜1，
∴A正确；
故选：A． 用反证法证明“三角形中至少有一个内角不小于60°”，应先假设这个三角形中（ ）
A. 有一个内角小于60° B. 每一个内角都小于60°
C. 有一个内角大于60° D. 每一个内角都大于60°
B
【解析】试题分析：此题要运用反证法，由题意先假设三角形的三个角都小于60°成立．然后推出不成立．得出选项．
【解析】
设三角形的三个角分别为：a，b，c．
假设，a＜60°，b＜60°，c＜60°，
则a+b+c＜60°+60°+60°，
即，a+b+c＜180°与三角形内角和定理a+b+c=180°矛盾．
所以假设不成立，即三角形中至少有一个角不小于60... 如图，在△ABC中，AB=AC，E是AB的中点，以点E为圆心，EB为半径画弧，交BC于点D，连接ED并延长到点F，使DF=DE，连接FC，若∠B=70°，则∠F的度数是（ ）
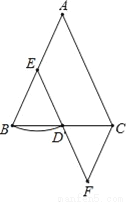
A. 40 B. 70 C. 50 D. 45
A
【解析】【解析】
∵以点E为圆心，EB为半径画弧，交BC于点D，∴EB=ED，∴∠EDB=∠B=70°，∴∠BED=180°﹣∠B=∠BDE=40°．
∵AB=AC，∴∠ACB=∠B，∴∠EDB=∠ACB，∴EF∥AC．
∵E是AB的中点，即BE=AE，∴BD=CD．
在△EBD和△FCD中，∵DE=DF，∠EDB=∠CDF，BD=CD，∴△EBD≌△FCD（SAS）... 如图所示的正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形，则点C的个数是（ ）
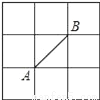
A. 6 B. 7 C. 8 D. 9
C
【解析】试题分析：如图：分情况讨论
①AB为等腰△ABC底边时，符合条件的C点有2个；
②AB为等腰△ABC其中的一条腰时，符合条件的C点有4个．
故选A． 如图,一艘海轮位于灯塔P南偏东70°方向的M处,它以每时40海里的速度向正北方向航行,2时后到达位于灯塔P北偏东40°方向的N处,则N处与灯塔P的距离为( )
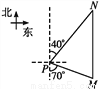
A. 40海里 B. 60海里
C. 70海里 D. 80海里
D
【解析】试题解析：MN=2×40=80（海里），
∵∠M=70°，∠N=40°，
∴∠NPM=180°-∠M-∠N=180°-70°-40°=70°，
∴∠NPM=∠M，
∴NP=MN=80（海里）．
故选D． 如图所示，在△ABC中，AB=AC，点D、E在BC边上，∠ABD=∠DAE=∠EAC=36°，则图中共有等腰三角形的个数是__．
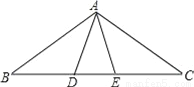
6
【解析】【解析】
∵AB=AC，∠ABD=36°，即△ABC是等腰三角形，∴∠C=∠B=36°，∴∠BAC=108°．
∵∠DAE=∠EAC=36°，∴∠BAD=36°，∴∠BAD=∠B=36°，∠EAC=∠C=36°，∴△ABD，△ACE是等腰三角形，∴∠ADE=∠AED=∠DAC=∠BAE=72°，∴△ADE，△ABE，△ACD是等腰三角形．
故答案为：6．
... 如图，在△ABC中，∠B与∠C的平分线交于点O，过点O作DE∥BC，分别交AB、AC于点D、E．若AB=5，AC=4，则△ADE的周长是__________．
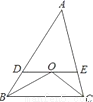
9
【解析】∵在△ABC中，∠B与∠C的平分线交于点O，
∴∠DBO＝∠CBO，∠ECO＝∠BCO，
∵DE∥BC，
∴∠DOB＝∠CBO，∠EOC＝∠BCO，
∴∠DBO＝∠DOB，∠ECO＝∠EOC，
∴OD＝BD，OE＝CE，
∵AB＝5，AC＝4，
∴△ADE的周长为：AD＋DE＋AE＝AD＋DO＋EO＋AE＝AD＋DB＋EC＋AE＝AB＋A... 如图，AD是△ABC的边BC上的高，由下列条件中的某一个就能推出△ABC是等腰三角形的是__．
①∠BAD=∠ACD；②∠BAD=∠CAD；③AB+BD=AC+CD；④AB﹣BD=AC﹣CD．
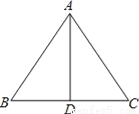
②③④
【解析】【解析】
应添加的条件是②③④；
证明：②当∠BAD=∠CAD时，∵AD是∠BAC的平分线，且AD是BC边上的高，则△ABD≌△ACD，∴△BAC是等腰三角形；
③延长DB至E，使BE=AB；延长DC至F，使CF=AC；连接AE、AF．
∵AB+BD=CD+AC，∴DE=DF，又AD⊥BC，∴△AEF是等腰三角形，∴∠E=∠F．
∵AB=BE，∴∠A... 证明题：如图所示，在△ABC中，AB=AC，∠APB≠∠APC，求证：PB≠PC．
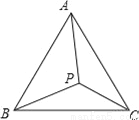
证明见解析.
【解析】试题分析：运用反证法进行求解．
试题解析：证明：假设PB≠PC不成立，则PB=PC．
在△ABP和△ACP中，∵AB=AC，AP=AP，BP=CP，∴△ABP≌△ACP，∴∠APB=∠APC．
与∠APB≠∠APC相矛盾．因而PB=PC不成立，则PB≠PC．