如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.
(1)用尺规作图方法,作∠ADC的平分线DN;(保留作图痕迹,不写作法和证明)
(2)设DN与AM交于点F,判断△ADF的形状.(只写结果)
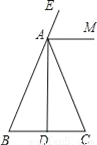
 (1)作图见解析;(2)△ADF是等腰直角三角形.
【解析】试题分析:(1)以D为圆心,以任意长为半径画弧,交AD于G,交DC于H,分别以G、H为圆心,以大于GH为半径画弧,两弧交于N,作射线DN,交AM于F.
(2)求出∠BAD=∠CAD,求出∠FAD=×180°=90°,求出∠CDF=∠AFD=∠ADF,推出AD=AF,即可得出答案.
【解析】
(1)如图所示:
(2...
(1)作图见解析;(2)△ADF是等腰直角三角形.
【解析】试题分析:(1)以D为圆心,以任意长为半径画弧,交AD于G,交DC于H,分别以G、H为圆心,以大于GH为半径画弧,两弧交于N,作射线DN,交AM于F.
(2)求出∠BAD=∠CAD,求出∠FAD=×180°=90°,求出∠CDF=∠AFD=∠ADF,推出AD=AF,即可得出答案.
【解析】
(1)如图所示:
(2... 已知∠AOB及其内部一点P,试讨论以下问题的解答:
(1)如图①,若点P在∠AOB的平分线上,我们可以过P点作直线垂直于角平分线,分别交OA、OB于点C、D,则可以得到△OCD是以CD为底边的等腰三角形;若点P不在∠AOB的平分线上(如图②),你能过P点作直线,分别交OA、OB于点C、D,得到△OCD是等腰三角形,且CD是底边吗?请你在图②中画出图形,并简要说明画法.
(2)若点P不在∠AOB的平分线上(如图③),我们可以过P点作PQ∥OA,并作∠QPR=∠AOB,直线PR分别交OA、OB于点C、D,则可以得到△OCD是以OC为底的等腰三角形.请你说明这样作的理由.
(3)若点P不在∠AOB的平分线上,请你利用在(2)中学到的方法,在图④中过P点作直线分别交OA、OB于点C、D,使得△OCD是等腰三角形,且OD是底边.保留画图的痕迹,不用写出画法.
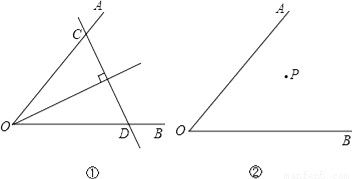
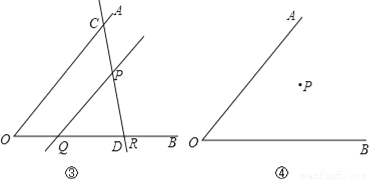
 (1)能,画法见解析;(2)理由见解析;(3)见解析.
【解析】试题分析:(1)作∠AOB的平分线,过P点作角平分线的垂线,分别交角的两边OA、OB于点C、D,则△OCD是以CD为底边的等腰三角形;
(2)根据PQ∥OA,得出∠QPR=∠OCD,进而得出OD=CD,即可得出答案;
(3)作QP∥DO,再作∠ODR=∠O,即可得出答案.
试题解析:【解析】
(1)能.
...
(1)能,画法见解析;(2)理由见解析;(3)见解析.
【解析】试题分析:(1)作∠AOB的平分线,过P点作角平分线的垂线,分别交角的两边OA、OB于点C、D,则△OCD是以CD为底边的等腰三角形;
(2)根据PQ∥OA,得出∠QPR=∠OCD,进而得出OD=CD,即可得出答案;
(3)作QP∥DO,再作∠ODR=∠O,即可得出答案.
试题解析:【解析】
(1)能.
... 已知x=2是不等式(x-5)(ax-3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是( )
A. a>1 B. a≤2 C. 1<a≤2 D. 1≤a≤2
 C
【解析】根据x=2是不等式(x-5)(ax-3a+2)≤0的解,可知(2-5)(2a-3a+2)≤0,解得:a≤2,再根据x=1不是这个不等式的解,可得(1-5)(a-3a+2)>0,解得:a>1,
由此可得a的取值范围为:1<a≤2.
故选:C.
C
【解析】根据x=2是不等式(x-5)(ax-3a+2)≤0的解,可知(2-5)(2a-3a+2)≤0,解得:a≤2,再根据x=1不是这个不等式的解,可得(1-5)(a-3a+2)>0,解得:a>1,
由此可得a的取值范围为:1<a≤2.
故选:C. 下列数值中不是不等式5x≥2x+9的解的是( )
A. 5 B. 4 C. 3 D. 2
 D
【解析】试题解析:移项得,5x﹣2x≥9,
合并同类项得,3x≥9,
系数化为1得,x≥3,
所以,不是不等式的解集的是x=2.
故选D.
D
【解析】试题解析:移项得,5x﹣2x≥9,
合并同类项得,3x≥9,
系数化为1得,x≥3,
所以,不是不等式的解集的是x=2.
故选D. 一元一次不等式2(x+1)≥4的解集在数轴上表示为( )
A.  B.
B.  C.
C. 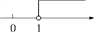 D.
D. 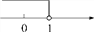
 A
【解析】试题分析:首先进行去括号可得:2x+2≥4,则2x≥2,解得:x≥1,在数轴上就是在1的右边,且表示1的点需要用实心点来表示.
A
【解析】试题分析:首先进行去括号可得:2x+2≥4,则2x≥2,解得:x≥1,在数轴上就是在1的右边,且表示1的点需要用实心点来表示. 如果(m+3)x>2m+6的解集为x<2,则m的取值范围是( )
A. m<0 B. m<-3 C. m>-3 D. m是任意实数
 B
【解析】由含有m的不等式(m+3)x>2m+6的解集为:x<2,根据不等式的基本性质3,可知m+3<0,解得m<-3.
故选:B.
B
【解析】由含有m的不等式(m+3)x>2m+6的解集为:x<2,根据不等式的基本性质3,可知m+3<0,解得m<-3.
故选:B. 不等式(a-2012)x>a-2012的解集是x<1.则a应满足的条件是( )
A. a=2012 B. a<2012 C. a>2012 D. 无法确定
 B
【解析】由含有a的不等式(a-2012)x>a-2012的解集为:x<1,根据不等式的基本性质3,可知a-2012<0,解得a<2012.
故选:B.
B
【解析】由含有a的不等式(a-2012)x>a-2012的解集为:x<1,根据不等式的基本性质3,可知a-2012<0,解得a<2012.
故选:B. 关于x的不等式(a-1)x>a-1的解集为x<1,则下列判断正确的是( )
A. a<0 B. a>1 C. a<1 D. a为任意数
 C
【解析】由含有a的不等式(a-1)x>a-1的解集为:x<1,根据不等式的基本性质3,可知a-1<0,解得a<1.
故选:C.
C
【解析】由含有a的不等式(a-1)x>a-1的解集为:x<1,根据不等式的基本性质3,可知a-1<0,解得a<1.
故选:C. 如果式子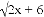 有意义,那么x的取值范围在数轴上表示出来,正确的是( )
有意义,那么x的取值范围在数轴上表示出来,正确的是( )
A.  B.
B. 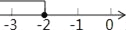 C.
C.  D.
D. 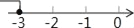
 C
【解析】试题分析:先根据二次根式的意义,其有意义的条件是被开方数大于等于0,因此可得2x+6≥0,可解不等式得x≥-3,因此可在数轴上表示为C.
故选C
C
【解析】试题分析:先根据二次根式的意义,其有意义的条件是被开方数大于等于0,因此可得2x+6≥0,可解不等式得x≥-3,因此可在数轴上表示为C.
故选C 已知x=2是不等式(x-5)(ax-3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是( )
A. a>1 B. a≤2 C. 1<a≤2 D. 1≤a≤2
 C
【解析】根据x=2是不等式(x-5)(ax-3a+2)≤0的解,可知(2-5)(2a-3a+2)≤0,解得:a≤2,再根据x=1不是这个不等式的解,可得(1-5)(a-3a+2)>0,解得:a>1,
由此可得a的取值范围为:1<a≤2.
故选:C.
C
【解析】根据x=2是不等式(x-5)(ax-3a+2)≤0的解,可知(2-5)(2a-3a+2)≤0,解得:a≤2,再根据x=1不是这个不等式的解,可得(1-5)(a-3a+2)>0,解得:a>1,
由此可得a的取值范围为:1<a≤2.
故选:C.