题目内容
下列数值中不是不等式5x≥2x+9的解的是( )
A. 5 B. 4 C. 3 D. 2
 D
【解析】试题解析:移项得,5x﹣2x≥9,
合并同类项得,3x≥9,
系数化为1得,x≥3,
所以,不是不等式的解集的是x=2.
故选D.
D
【解析】试题解析:移项得,5x﹣2x≥9,
合并同类项得,3x≥9,
系数化为1得,x≥3,
所以,不是不等式的解集的是x=2.
故选D.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果两个直角三角形的两条直角边对应相等,那么这两个直角三角形全等的依据是( )
A. SSS B. AAS C. SAS D. HL
 C
【解析】【解析】
两边及夹角对应相等的两个三角形全等,这为“边角边”定理,简写成“SAS”.故选C.
C
【解析】【解析】
两边及夹角对应相等的两个三角形全等,这为“边角边”定理,简写成“SAS”.故选C. 在图形平移的过程中,下列说法中错误的是( )
A. 图形上任意点移动的方向相同 B. 图形上任意点移动的距离相同
C. 图形上可能存在不动的点 D. 图形上任意两点连线的长度不变
 C
【解析】试题解析:平移的时候,图形上的任何一个点都移动,而且移动的方向和距离都相同.
故选C.
C
【解析】试题解析:平移的时候,图形上的任何一个点都移动,而且移动的方向和距离都相同.
故选C. 下列各数中,不是不等式2-3x>5的解的是( )
A. -2 B. -3 C. -1 D. -1.35
 C
【解析】解不等式2-3x>5可得x<-1,因此可知-1不是不等式2-3x>5的解.
故选:C.
C
【解析】解不等式2-3x>5可得x<-1,因此可知-1不是不等式2-3x>5的解.
故选:C. 如果式子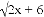 有意义,那么x的取值范围在数轴上表示出来,正确的是( )
有意义,那么x的取值范围在数轴上表示出来,正确的是( )
A.  B.
B. 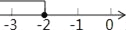 C.
C.  D.
D. 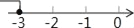
 C
【解析】试题分析:先根据二次根式的意义,其有意义的条件是被开方数大于等于0,因此可得2x+6≥0,可解不等式得x≥-3,因此可在数轴上表示为C.
故选C
C
【解析】试题分析:先根据二次根式的意义,其有意义的条件是被开方数大于等于0,因此可得2x+6≥0,可解不等式得x≥-3,因此可在数轴上表示为C.
故选C 如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形的是__.
①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD;④AB﹣BD=AC﹣CD.
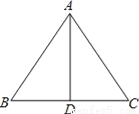
 ②③④
【解析】【解析】
应添加的条件是②③④;
证明:②当∠BAD=∠CAD时,∵AD是∠BAC的平分线,且AD是BC边上的高,则△ABD≌△ACD,∴△BAC是等腰三角形;
③延长DB至E,使BE=AB;延长DC至F,使CF=AC;连接AE、AF.
∵AB+BD=CD+AC,∴DE=DF,又AD⊥BC,∴△AEF是等腰三角形,∴∠E=∠F.
∵AB=BE,∴∠A...
②③④
【解析】【解析】
应添加的条件是②③④;
证明:②当∠BAD=∠CAD时,∵AD是∠BAC的平分线,且AD是BC边上的高,则△ABD≌△ACD,∴△BAC是等腰三角形;
③延长DB至E,使BE=AB;延长DC至F,使CF=AC;连接AE、AF.
∵AB+BD=CD+AC,∴DE=DF,又AD⊥BC,∴△AEF是等腰三角形,∴∠E=∠F.
∵AB=BE,∴∠A... 下列选项中,可以用来证明命题“若a2>1,则a>1”是假命题的反例是( )
A. a=﹣2 B. a=﹣1 C. a=1 D. a=2
 A
【解析】试题分析:此题主要考查了利用举例法证明一个命题错误,要说明数学命题的错误,只需举出一个反例即可这是数学中常用的一种方法.根据要证明一个结论不成立,可以通过举反例的方法来证明一个命题是假命题.
用来证明命题“若a2>1,则a>1”是假命题的反例可以是:a=-2,
∵(-2)2>1,但是a=-2<1,
∴A正确;
故选:A.
A
【解析】试题分析:此题主要考查了利用举例法证明一个命题错误,要说明数学命题的错误,只需举出一个反例即可这是数学中常用的一种方法.根据要证明一个结论不成立,可以通过举反例的方法来证明一个命题是假命题.
用来证明命题“若a2>1,则a>1”是假命题的反例可以是:a=-2,
∵(-2)2>1,但是a=-2<1,
∴A正确;
故选:A. 用提公因式法分解因式: 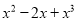 =__________
=__________
 【解析】根据提公因式法可以得到.
故答案为: .
【解析】根据提公因式法可以得到.
故答案为: . 在如图所示的2×2方格中,连接AB、AC,则∠1+∠2=_____度.
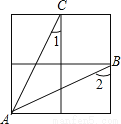
 90°
【解析】在△ACM和△BAN中,AN=CM,∠AMC=∠BNA,CM=AN
∴△ACM≌△BAN,
∴∠2=∠CAM,即可得∠1+∠2=90°.故答案为:90°.
90°
【解析】在△ACM和△BAN中,AN=CM,∠AMC=∠BNA,CM=AN
∴△ACM≌△BAN,
∴∠2=∠CAM,即可得∠1+∠2=90°.故答案为:90°. 
