题目内容
一元一次不等式2(x＋1)≥4的解集在数轴上表示为( )
A. 
B. 
C. 
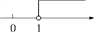D.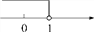 
A
【解析】试题分析：首先进行去括号可得：2x+2≥4，则2x≥2，解得：x≥1，在数轴上就是在1的右边，且表示1的点需要用实心点来表示.
练习册系列答案
相关题目
如图，在△ABC中，∠C=60°，∠B=50°，D是BC上一点，DE⊥AB于点E，DF⊥AC于点F，则∠EDF的度数为（ ）
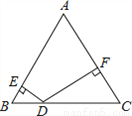
A. 90° B. 100° C. 110° D. 120°
C
【解析】【解析】
在△ABC中，∵∠C=60°，∠B=50°，∴∠A=70°．
∵DE⊥AB于点E，DF⊥AC于点F，∴∠AED=∠AFD=90°，∴∠EDF=360°﹣∠A﹣∠AED﹣∠AFD=110°．故选C． 下列说法正确的是( )
A. 平移改变图形的形状
B. 平移改变图形的大小
C. 平移改变物体的形状和大小
D. 平移不改变物体的形状和大小
D
【解析】试题解析：平移的特点是不变形，即平移不改变物体的形状和大小.
故选D. 下列说法正确的有（ ）
①4是x﹣3＞1的解；②不等式x﹣2＜0的解有无数个；③x＞5是不等式x+2＞3的解集；④x=3是不等式x+2＞1的解；⑤不等式x+2＜5有无数个正整数解．
A．1个 B．2个 C．3个 D．4个
B.
【解析】
试题分析：解x﹣3＞1得：x＞4，所以4不是x﹣3＞1的解，故①错误；不等式x﹣2＜0的解有无数个，此说法正确，故②正确；解不等式x+2＞3得：x＞1，所以x＞5不是不等式x+2＞3的解集，故③错误；解不等式x+2＞1得：x＞-1,所以x=3是不等式x+2＞1的解，故④正确；解不等式x+2＜5得：x＜3,所以其正整数解为1，2共2个.故⑤错误.
故选B. 已知x=2是不等式（x-5）（ax-3a+2）≤0的解，且x=1不是这个不等式的解，则实数a的取值范围是（ ）
A. a＞1 B. a≤2 C. 1＜a≤2 D. 1≤a≤2
C
【解析】根据x=2是不等式（x-5）（ax-3a+2）≤0的解，可知（2-5）（2a-3a+2）≤0，解得：a≤2，再根据x=1不是这个不等式的解，可得（1-5）（a-3a+2）＞0，解得：a＞1，
由此可得a的取值范围为：1＜a≤2．
故选：C. 证明题：如图所示，在△ABC中，AB=AC，∠APB≠∠APC，求证：PB≠PC．
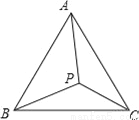
证明见解析.
【解析】试题分析：运用反证法进行求解．
试题解析：证明：假设PB≠PC不成立，则PB=PC．
在△ABP和△ACP中，∵AB=AC，AP=AP，BP=CP，∴△ABP≌△ACP，∴∠APB=∠APC．
与∠APB≠∠APC相矛盾．因而PB=PC不成立，则PB≠PC． 用反证法证明“三角形中至少有一个内角不小于60°”，应先假设这个三角形中（ ）
A. 有一个内角小于60° B. 每一个内角都小于60°
C. 有一个内角大于60° D. 每一个内角都大于60°
B
【解析】试题分析：此题要运用反证法，由题意先假设三角形的三个角都小于60°成立．然后推出不成立．得出选项．
【解析】
设三角形的三个角分别为：a，b，c．
假设，a＜60°，b＜60°，c＜60°，
则a+b+c＜60°+60°+60°，
即，a+b+c＜180°与三角形内角和定理a+b+c=180°矛盾．
所以假设不成立，即三角形中至少有一个角不小于60...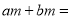 
m(_________)
【解析】根据提公因式法因式分解，提取公因式m可得m（a+b）.
故答案为：a+b. 已知：如图，点C为AB中点，CD=BE，CD∥BE.求证:△ACD≌△CBE.
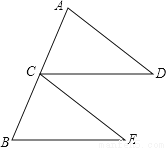
证明见解析.
【解析】试题分析：根据中点定义求出AC=CB，根据两直线平行，同位角相等，求出∠ACD=∠B，然后利用SAS即可证明△ACD≌△CBE．
试题解析：证明：∵CD∥BE，∴∠ACD=∠B..
∵点C为AB中点，∴AC=CB.
又∵CD=BE，∴△ACD≌△CBE（SAS）