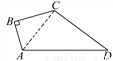
如图，∠B＝90°，AB＝3，BC＝4，CD＝12，AD＝13.求四边形ABCD的面积．
36.
【解析】试题分析：连接AC，在直角三角形ABC中，由AB及BC的长，利用勾股定理求出AC的长，再由AD及CD的长，利用勾股定理的逆定理得到三角形ACD为直角三角形，根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积，即可求出四边形的面积．
试题解析：【解析】
连接AC．如图所示：
∵∠B=90°，∴△ABC为直角三角形．又∵AB=3，BC=4，∴根... 如图，在等腰三角形ABC中，∠ABC=90°，D为AC边上中点，过D点作DE⊥DF，交AB于E，交BC于F，若AE=4，FC=3，求EF长．
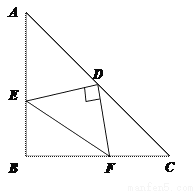
连结BD，证△BED≌△CFD和△AED≌△BFD，得BF=4，BE=3，再运用勾股定理求得EF=5 如果m＜n＜0，那么下列结论中错误的是（ ）
A、m－9＜n－9 B、－m＞－n C、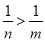
D、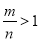
C
【解析】
试题分析：根据不等式的基本性质依次分析各项即可.
m＜n＜0，
∴m－9＜n－9，－m＞－n，，，
故选C. 若a－b＜0，则下列各式中一定正确的是（ ）
A、a＞b B、ab＞0 C、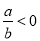
D、－a＞－b
D
【解析】
试题分析：由a－b＜0可得a＜b，再根据不等式的基本性质依次分析各项即可.
a－b＜0，
∴a＜b，
∴－a＞－b，但无法确定ab与的符号，
故选D. 由不等式ax＞b可以推出x＜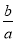
，那么a的取值范围是（ ）
A、a≤0 B、a＜0 C、a≥0 D、a＞0
B
【解析】
试题分析：根据不等式的基本性质即可判断.
由不等式ax＞b推出x＜，可知a＜0，
故选B. 如果t＞0，那么a＋t与a的大小关系是（ ）
A、a＋t＞a B、a＋t＜a C、a＋t≥a D、不能确定
A
【解析】
试题分析：根据不等式的基本性质即可得到结果.
t＞0，
∴a＋t＞a，
故选A. 如果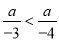
，则a必须满足（ ）
A、a≠0 B、a＜0 C、a＞0 D、a为任意数
C
【解析】
试题分析：根据不等式的基本性质即可判断.
，
∴a＞0，
故选C. 已知有理数a、b、c在数轴上的位置如图所示，则下列式子正确的是（ ）
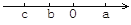
A. cb＞ab B. ac＞ab C. cb＜ab D. c＋b＞a＋b
A
【解析】试题分析：先根据数轴的特点得出a＞0＞b＞c，再根据不等式的性质进行判断：
A、∵a＞0＞b＞c，∴cb＞0＞ab. 选项正确.
B、∵c＜b，a＞0，∴ac＜ab. 选项错误.
C、∵c＜a，b＜0，∴cb＞ab. 选项错误.
D、∵c＜a，∴c+b＜a+b. 选项错误.
故选A． 有下列说法：
（1）若a＜b，则－a＞－b； （2）若xy＜0，则x＜0，y＜0；
（3）若x＜0，y＜0，则xy＜0； （4）若a＜b，则2a＜a＋b；
（5）若a＜b，则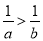
； （6）若
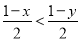，则x＞y.
其中正确的说法有（ ）
A、2个 B、3个 C、4个 D、5个
B
【解析】
试题分析：根据不等式的基本性质依次分析各项即可。
（1）若a＜b，则－a＞－b，正确；
（2）若xy＜0，则x＜0，y＞0或x＞0，y＜0，错误；
（3）若x＜0，y＜0，则xy＞0，错误；
（4）若a＜b，则2a＜a＋b，正确；
（5）若a＜0＜b，则，错误；
（6）若，则x＞y，正确.
故选B. 2a与3a的大小关系（ ）
A、2a＜3a B、2a＞3a C、2a＝3a D、不能确定
D
【解析】
试题分析：题目中没有明确a的正负，故要分情况讨论.
当时，；当时，；当时，，
故选D.