题目内容
如果m＜n＜0，那么下列结论中错误的是（ ）
A、m－9＜n－9 B、－m＞－n C、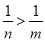
D、
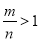
C
【解析】
试题分析：根据不等式的基本性质依次分析各项即可.
m＜n＜0，
∴m－9＜n－9，－m＞－n，，，
故选C.
练习册系列答案
相关题目
四位学生用计算器求sin62°20′的值正确的是（ ）
A. 0.8857 B. 0.8856 C. 0.8852 D. 0.8851
A
【解析】试题解析：
故选A. 如图，在数轴上所表示的是哪一个不等式的解集（ ）
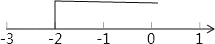
A．
＞﹣1 B．
≥﹣3 C．x+1≥﹣1 D．﹣2x＞4
C
【解析】
试题分析：依题意得：数轴表示的解集是：x≥﹣2；解＞﹣1得：x＞﹣2；解≥﹣3，得x+3≥﹣6，不等式的解集是x≥﹣9；解x+1≥﹣1得：x≥﹣2；解﹣2x＞4得x＜﹣2.
故应选C． 满足－2x＞－12的非负整数有________________________．
0，1，2，3，4，5
【解析】∵不等式-2x＞-12的解为x＜6，∴满足x＜6的非负整数有0，1，2，3，4，5． 已知有理数a、b、c在数轴上的位置如图所示，则下列式子正确的是（ ）
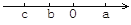
A. cb＞ab B. ac＞ab C. cb＜ab D. c＋b＞a＋b
A
【解析】试题分析：先根据数轴的特点得出a＞0＞b＞c，再根据不等式的性质进行判断：
A、∵a＞0＞b＞c，∴cb＞0＞ab. 选项正确.
B、∵c＜b，a＞0，∴ac＜ab. 选项错误.
C、∵c＜a，b＜0，∴cb＞ab. 选项错误.
D、∵c＜a，∴c+b＜a+b. 选项错误.
故选A． 已知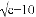
＋|a－6|＋(b－8)2＝0，则以a、b、c为三边的三角形是__________.
直角三角形
【解析】【解析】
∵，∴a-6=0， b-8=0，c-10=0，∴a=6，b=8，c=10，
∴a2+b2=c2，∴以a、b、c为三边的三角形是直角三角形．故答案为：直角． 下列四组线段中，能组成直角三角形的是（ ）
A. a=1，b=2，c=3 B. a=4，b=2，c=3
C. a=4，b=2，c=5 D. a=4，b=5，c=3
D
【解析】试题分析：A．∵，∴不能构成直角三角形，故本选项错误；
B．∵，∴不能构成直角三角形，故本选项错误；
C．∵，∴不能构成直角三角形，故本选项错误；
D．∵，∴能构成直角三角形，故本选项正确．
故选D． 在△ABC中，AB=AC，若∠A=40°，则∠B=__________度.
70
【解析】∵AB=AC，
∴∠B=∠C，
∵∠A=40°，
∴∠B=∠C=(180?40)=70°，
故答案为：70. 如图，已知正方形ABCD的边长为2，如果将线段BD绕着点B旋转后，点D落在CB的延长线上的D′处，那么tan∠BAD′＝________.
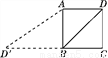
【解析】由题知，∠ABD′=90°，BD=BD′==2，，
∴tan∠BAD′==，
故答案为： .