下列各式分别在什么条件下成立？
（1）a＞－a； （2）a2＞a； （3）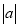
＞a．
（1）a＞0；（2）a＞l或a＜0；（3）a<0．
【解析】分析：根据不等式的基本性质进行判断即可.
本题解析：
(1)在不等式a＞-a的两边同时加上a，得到2a＞0，再在不等式的两边同时除以2，得到a＞0，即当a＞0时，不等式a＞-a成立；
(2)在不等式a2＞a的两边同时减去a，得到a（a-1）＞0，所以
或，
解得a＞l或a＜0．
即当a＞l或a＜0时，不等式a2＞... 有两个分数A=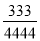
，B=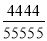
，问：A与B哪个大？
A＜B
【解析】分析：求出两个数的倒数，根据倒数即可比较两个数的大小．
本题解析：∵=×=×（10＋）=12．5＋＜13
==（10＋）=13．33＋＞13
∴＞＞0 ∴A＜B 下列数值中，是不等式x－2＞2的一个解的是( )
A. 0 B. 2
C. 4 D. 6
D
【解析】解不等式x?2>2，得x>4，
而大于4的数只有6.
故选D. 不等式x－3＞1的解集是( )
A. x＞2 B. x＞4 C. x＞－2 D. x＞－4
B
【解析】试题分析：根据不等式的基本性质即可得到结果.
x－3＞1
x＞4
故选B. 下列不等式中，不含有x＝－1这个解的是
A. 2x＋1≤－3 B. 2x－1≥－3
C. －2x＋1≥3 D. －2x－1≤3
A
【解析】A. ∵ 2x＋1≤－3 ，∴x≤-2，∴不含有x＝－1这个解;
B. ∵ 2x－1≥－3，∴x≥-1，∴含有x＝－1这个解
C. ∵－2x＋1≥3 ，∴x≤-1，∴含有x＝－1这个解
D. ∵－2x－1≤3，∴x≥-2，∴含有x＝－1这个解
故选A. 不等式3x＜6的解集是_____；使该不等式成立的正整数解是___，当_____时，不等式3x＞7不成立．
x＜2 1 x≤
【解析】3x＜6的解集为x<2；
其正整数解为1，
当x≤时，不等式3x＞7不成立.
故答案为(1). x＜2 (2). 1 (3). x≤ 根据已知条件写出相应不等式．
(1)－3，－2，－1,0,1都是不等式的解；
(2)不等式的负整数解只有－1，－2，－3；
(3)不等式的解的最大的值是0.
见解析
【解析】分析：根据题中的条件，得出每个小题中的数据在不等式的解集范围内即可.
本题解析：
(1)∵不等式有五个连续的整数解，
∴求不等式x-1≤0的五个最大整数解。
(2)∵不等式有三个连续的负整数解
∴求不等式2(x+1) ≤0的三个最大负整数解。
(3)∵不等式的解的最大的值是0，
∴求不等式x-1<0的最大整数解。 对于解不等式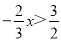
，正确的结果是（ ）
A．x＜
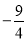B．x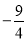＞ C．x＞-1 D．x＜-1
A．
【解析】
试题分析：先去分母得，-4x＞9，再把x的系数化为1得，x＜．
故选A． 若不等式(a－3)x＞1的解集为x＜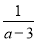
，则a的取值范围是_____.
a＜3
【解析】∵(a?3)x>1的解集为x<，
∴不等式两边同时除以(a?3)时不等号的方向改变，
∴a?3<0，
∴a<3.
故答案为：a<3. 根据不等式的基本性质，求出下列不等式的解集．
(1) 
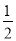x＞－3；
(2)3x－6≤0；
(3)－12x＋6＞0.
(1) x＞－6. (2) x≤2. (3) x＜.
【解析】分析：根据不等式的性质即可求解.
本题解析： (1)两边都乘以2，得x＞－6.
(2)两边都加上6，得3x≤6.两边都除以3，得x≤2.
(3)两边都减去6，得－12x＞－6.两边都除以－12，得x＜.