题目内容
下列不等式中，不含有x＝－1这个解的是
A. 2x＋1≤－3 B. 2x－1≥－3
C. －2x＋1≥3 D. －2x－1≤3
A
【解析】A. ∵ 2x＋1≤－3 ，∴x≤-2，∴不含有x＝－1这个解;
B. ∵ 2x－1≥－3，∴x≥-1，∴含有x＝－1这个解
C. ∵－2x＋1≥3 ，∴x≤-1，∴含有x＝－1这个解
D. ∵－2x－1≤3，∴x≥-2，∴含有x＝－1这个解
故选A.
练习册系列答案
相关题目
如图（1）将△ABD平移，使D沿BD延长线移至C得到△A′B′D′，A′B′交AC于E，AD平分∠BAC．
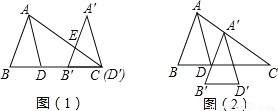
（1）猜想∠B′EC与∠A′之间的关系，并写出理由．
（2）如图将△ABD平移至如图（2）所示，得到△A′B′D′，请问：A′D平分∠B′A′C吗？为什么？
（1）∠B′EC=2∠A′；（2）A′D′平分∠B′A′C．见解析
【解析】
试题分析：（1）根据平移的性质得出∠BAD=∠DAC，∠BAD=∠A′，AB∥A′B′，进而得出∠BAC=∠B′EC，进而得出答案；
（2）利用平移的性质得出∠B′A′D′=∠BAD，AB∥A′B′，进而得出∠BAD=∠BAC，即可得出∠B′A′D′=∠B′A′C．
【解析】
（1）∠B′EC=... 在一次实验中，小明把一根弹簧的上端固定、在其下端悬挂物体，下面是测得的弹簧的长度y与所挂物体质量x的一组对应值．
所挂物体质量x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧长度y/cm | 18 | 20 | 22 | 24 | 26 | 28 |
①上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
②当所挂物体重量为3千克时，弹簧多长？不挂重物时呢？
③若所挂重物为7千克时（在允许范围内），你能说出此时的弹簧长度吗？
①上表反映了弹簧长度与所挂物体质量之间的关系；其中所挂物体质量是自变量，弹簧长度是因变量；②当所挂物体重量为3千克时，弹簧长24厘米；当不挂重物时，弹簧长18厘米；③32厘米．
【解析】试题分析：①因为表中的数据主要涉及到弹簧的长度和所挂物体的质量，所以反映了所挂物体的质量和弹簧的长度之间的关系，所挂物体的质量是自变量；弹簧的长度是因变量；
②由表可知，当物体的质量为3kg时，弹簧的长... 如图,在△ABC中,AB=AC,AD=BD=BC,则∠A的度数是( )
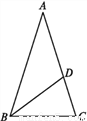
A. 30° B. 36° C. 45° D. 20°
B
【解析】【解析】
设∠A=x°．∵BD=AD，∴∠A=∠ABD=x°，∠BDC=∠A+∠ABD=2x°．
∵BD=BC，∴∠BDC=∠BCD=2x°．
∵AB=AC，∴∠ABC=∠BCD=2x°．
在△ABC中，x+2x+2x=180，解得：x=36，∴∠A=36°．
故选B． 根据不等式的基本性质，求出下列不等式的解集．
(1) 
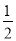x＞－3；
(2)3x－6≤0；
(3)－12x＋6＞0.
(1) x＞－6. (2) x≤2. (3) x＜.
【解析】分析：根据不等式的性质即可求解.
本题解析： (1)两边都乘以2，得x＞－6.
(2)两边都加上6，得3x≤6.两边都除以3，得x≤2.
(3)两边都减去6，得－12x＞－6.两边都除以－12，得x＜. 若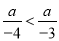
，试判断a的正负性．
a为负数
【解析】分析：先根据不等式基本性质3,两边都乘以,再根据不等式基本性质1,两边都减去3a即可得出结论.
本题解析：根据不等式基本性质3，两边都乘以－12，得3a＞4a．
根据不等式基本性质1，两边都减去3a，得0＞a ，即a<0 ，即a为负数． x＜y得到ax＞ay的条件应是____________．
a＜0
【解析】∵x＜y得到ax＞ay是两边同时乘以a，不等号的方向发生了改变，∴a＜0． 如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（ ）
A. 
B. 
C. 4 D. 5
C
【解析】试题分析：设BN=x，由折叠的性质可得DN=AN=9－x，
∵D是BC的中点，
∴BD=3，
在Rt△BDN中，x2+32=（9－x）2，
解得x=4．
故线段BN的长为4．
故选C． 在△ABC中，已知AC=3，BC=4，AB=5，那么下列结论正确的是( )
A.sinA=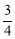
B.cosA=
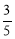C.tanA= 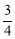D.cos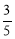B=
B
【解析】
试题分析：先根据勾股定理的逆定理判断△ABC的形状，再根据三角函数的定义依次分析各项即可.
∵
∴△ABC是直角三角形
∴，，，
故选B.