题目内容
若不等式(a－3)x＞1的解集为x＜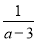
，则a的取值范围是_____.
a＜3
【解析】∵(a?3)x>1的解集为x<，
∴不等式两边同时除以(a?3)时不等号的方向改变，
∴a?3<0，
∴a<3.
故答案为：a<3.
练习册系列答案
相关题目
如图，直线AB与CD相交于点O，∠AOD=50°，则∠BOC=__________．
50
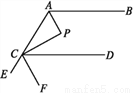
【解析】根据对顶角相等，易得∠BOC=50° 如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.
(1)用α表示∠ACP;
(2)求证:AB∥CD;
(3)若AP∥CF,求证:FC平分∠DCE.
（1）∠CAP=90°-α； （2）证明见解析；（3）证明见解析；
【解析】试题分析：（1）由角平分线的定义可得∠PAC=α，在Rt△PAC中根据直角三角形的性质可求得∠ACP；
（2）结合（1）可求得∠ACD，可证明∠ACD+∠BAC=180°，可证明AB∥CD；
（3）由平行线的性质可得∠ECF=∠CAP，∠ECD=∠CAB，结合条件可证得∠ECF=∠FCD，可证得结论．
... 下列运算正确的是( )
A. (-2ab)·(-3ab)3=-54a4b4 B. 5x2·(3x3)2=15x12
C. (-0.1b)·(-10b2)3=-b7 D. (2×10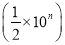n) 
=102n
D
【解析】解：A． 原式=54a4b4，故A错误；
B．原式=45x8，故B错误；
C． 原式=100b7，故C错误；
D．正确．
故选D． 用A、B两种型号的钢丝各两根分别作为长方形的长与宽，焊接成周长不小于2.4m的长方形框架，已知每根A型钢丝的长度比每根B型钢丝长度的2倍少3cm.
(1)设每根B型钢丝长为xcm，按题意列出不等式并求出它的解集；
(2)如果每根B型钢丝长度有以下四种选择：30cm,40cm,41cm,45cm，那么哪些合适？
（1）x≥41；（2）41cm,45cm合适
【解析】分析：设B的一边长度为x，则A的一边为2x-3; 然后根据题意列出不等式可求出x的范围即可．再讨论可解.
本题解析：
【解析】
(1) (1)设每根B型号的铁丝x厘米，每根A型铁丝的长度比每根B型钢丝的长度的2倍小3cm，所以A型号的铁丝长为2x－3厘米
2(2x－3)＋2x≥240，∴x≥41
(2) ∵每根B... 不等式x－3＞1的解集是( )
A. x＞2 B. x＞4 C. x＞－2 D. x＞－4
B
【解析】试题分析：根据不等式的基本性质即可得到结果.
x－3＞1
x＞4
故选B. 如果x－7＜－5，则x__________；如果－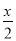
＞0，那么x_________．
＜2 ＜0
【解析】根据不等式的基本性质1，不等式x?70两边同时乘以?2,不等号的方向改变,则如果?>0，那么x<0.
故答案为：<2；<0. （10分）如图所示，某公路一侧有A、B两个送奶站，C为公路上一供奶站，CA和CB为供奶路线，现已测得AC＝8km，BC＝15km，AB＝17km，∠1＝30°，若有一人从C处出发，沿公路边向右行走，速度为2.5km/h，问：多长时间后这个人距B送奶站最近？
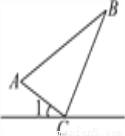
3h.
【解析】试题分析：首先根据勾股定理逆定可证明△ABC是直角三角形，然后计算出∠BCD的度数，再根据直角三角形的性质算出DC的长，然后根据速度和路程可计算出多长时间后这人距离B送奶站最近．
试题解析：【解析】
过B作BD⊥公路于D．∵82+152=172，∴AC2+BC2=AB2，∴△ABC是直角三角形，且∠ACB=90°．
∵∠1=30°，∴∠BCD=180°-90°-... 如图所示，P是正方形ABCD内一点，将△ABP绕点B顺时针方向旋转能与△CBP′重合，若PB＝2，则PP′＝_______.
【解析】【解析】
∵四边形ABCD为正方形，∴∠ABC=90°．∵△ABP绕点B顺时针方向旋转能与△CBP′重合，∴∠PBP′=∠ABC=90°，PB=P′B=2，∴△PBP′为等腰直角三角形，∴PP′=PB=．
故答案为： ．