利用基本作图方法,不能作出唯一三角形的是( )
A. 已知两边及其夹角 B. 已知两角及其夹边
C. 已知两边及一边的对角 D. 已知三边
 C
【解析】A. 已知两边及其夹角,作图依据 “SAS”; B. 已知两角及其夹边,作图依据 “ASA”;C. 已知两边及一边的对角,不能做出唯一的三角形; D. 已知三边,作图依据 “SSS”.故选C.
C
【解析】A. 已知两边及其夹角,作图依据 “SAS”; B. 已知两角及其夹边,作图依据 “ASA”;C. 已知两边及一边的对角,不能做出唯一的三角形; D. 已知三边,作图依据 “SSS”.故选C. 根据下列已知条件,能唯一画出△ABC的是( )
A. ∠A=36°,∠B=45°,AB=4 B. AB=4,BC=3,∠A=30°
C. AB=3,BC=4,CA=1 D. ∠C=90°,AB=6
 A
【解析】A. ∠A=36°,∠B=45°,AB=4,利用原理“ASA”可以画出唯一的三角形;B、C、D都不能唯一的作出三角形.故选A.
A
【解析】A. ∠A=36°,∠B=45°,AB=4,利用原理“ASA”可以画出唯一的三角形;B、C、D都不能唯一的作出三角形.故选A. 如图,小敏做试题时,不小心把题目中的三角形用墨水弄污了一部分,她想在一块白纸上作一个完全一样的三角形,

然后粘贴在上面,她作图的依据是( )
A. SSS B. SAS C. ASA D. AAS
 C
【解析】根据图形,可以确定两角及其夹边.故选C.
C
【解析】根据图形,可以确定两角及其夹边.故选C. 下列尺规作图,能判断AD是△ABC边上的高是( )
A. 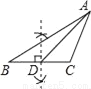 B.
B. 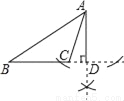 C.
C. 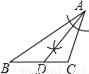 D.
D. 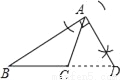
 B
【解析】试题分析:过点A作BC的垂线,垂足为D,故选B.
B
【解析】试题分析:过点A作BC的垂线,垂足为D,故选B. 如图,已知线段a,b和∠α=40°,你能作出符合如下要求的唯一三角形吗?AB=a,BC=b,∠A=∠α,若能,写出作法;若不能,请说明理由.
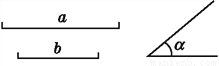
 见解析
【解析】【试题分析】AB=a,BC=b,∠A=∠α,已知两边及其一边的对角,不能作出唯一的三角形.如下图.
【试题解析】
如图,能作出两个三角形:△ABC'和△ABC,所以不能作出唯一的符合要求的三角形.
理由:SSA不能说明两个三角形全等,所以一般情况下,已知两边和其中一边的对角不能作出唯一的三角形.
见解析
【解析】【试题分析】AB=a,BC=b,∠A=∠α,已知两边及其一边的对角,不能作出唯一的三角形.如下图.
【试题解析】
如图,能作出两个三角形:△ABC'和△ABC,所以不能作出唯一的符合要求的三角形.
理由:SSA不能说明两个三角形全等,所以一般情况下,已知两边和其中一边的对角不能作出唯一的三角形. 如图是数轴的一部分,其单位长度为a,已知在△ABC中,AB=3a,BC=4a,AC=5a.用直尺和圆规作出△ABC(要求:使点A,C在数轴上,保留作图痕迹,不必写出作法).

 见解析
【解析】【试题分析】利用“SSS”作出三角形,作图方法见解析.
【试题解析】
如图.
作法如下:
(1)在数轴上截取AC=5a.
(2)分别以A,C为圆心,以3a,4a为半径画弧,两弧相交于点B.
(3)连接AB,BC,则△ABC即为所求作的三角形.
见解析
【解析】【试题分析】利用“SSS”作出三角形,作图方法见解析.
【试题解析】
如图.
作法如下:
(1)在数轴上截取AC=5a.
(2)分别以A,C为圆心,以3a,4a为半径画弧,两弧相交于点B.
(3)连接AB,BC,则△ABC即为所求作的三角形. 如图,已知线段a,c,∠α.
求作△ABC,使BC=a,AB=c,∠ABC=∠α.
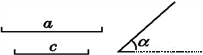
 见解析
【解析】【试题分析】利用“SAS”原理作图.
【试题解析】
(1)作∠MBN=∠α.
(2)在射线BM上截取BA=c,在射线BN上截取BC=a.
(3)连接AC,则△ABC即为所求作的三角形(如图).
见解析
【解析】【试题分析】利用“SAS”原理作图.
【试题解析】
(1)作∠MBN=∠α.
(2)在射线BM上截取BA=c,在射线BN上截取BC=a.
(3)连接AC,则△ABC即为所求作的三角形(如图). 如图,已知∠α,∠β且∠α>∠β.求作∠γ,使∠γ=∠α-∠β.
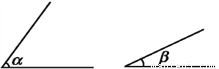
 见解析
【解析】【试题分析】运用基本作图“作一个角等于已知角”,作出∠α,∠β,根据两角之差即可.
【试题解析】
如图.
(1)作射线OA.
(2)以OA为一边,作∠BOA,使∠BOA=∠α.
(3)以OB为一边在∠AOB内作∠BOC,使∠BOC=∠β,则∠AOC=∠α-∠β.故∠AOC=∠γ就是所求作的角.
见解析
【解析】【试题分析】运用基本作图“作一个角等于已知角”,作出∠α,∠β,根据两角之差即可.
【试题解析】
如图.
(1)作射线OA.
(2)以OA为一边,作∠BOA,使∠BOA=∠α.
(3)以OB为一边在∠AOB内作∠BOC,使∠BOC=∠β,则∠AOC=∠α-∠β.故∠AOC=∠γ就是所求作的角. 市政建筑公司要在学校东面分别建造一座桥和一个汽车站(汽车站在学校的正东方向),桥在汽车站北面,现已知学校到桥、桥到汽车站及学校到汽车站的距离分别为500 m,500 m,250 m,请根据以上信息确定桥与汽车站应分别建在何处,在下面图纸上标出来(不写作法,保留作图痕迹);这三个场所构成一个什么形状的三角形?
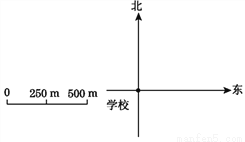
 见解析
【解析】【试题分析】根据单位长度,画出图形即可.
【试题解析】
如图,A为汽车站的位置,B为桥的位置,这三个场所构成一个等腰三角形.
见解析
【解析】【试题分析】根据单位长度,画出图形即可.
【试题解析】
如图,A为汽车站的位置,B为桥的位置,这三个场所构成一个等腰三角形. “综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度.
(1)用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形.请列举出所有满足条件的三角形.
(2)用直尺和圆规作出三边满足a<b<c的三角形(用给定的单位长度,不写作法,保留作图痕迹).
 (1)答案见解析;(2)作图见解析.
【解析】试题分析:根据三角形的三边关系得出所有的结果;根据三角形的画法画出三角形.
试题解析:(1)共九种:(2,2,2)(2,2,3)(2,3,3)(2,3,4)(2,4,4)(3,3,3)(3,3,4)(3,4,4)(4,4,4)
(2)只有a=2,b=3,c=4的一个三角形,如图所示的△ABC就是满足条件的三角形
(1)答案见解析;(2)作图见解析.
【解析】试题分析:根据三角形的三边关系得出所有的结果;根据三角形的画法画出三角形.
试题解析:(1)共九种:(2,2,2)(2,2,3)(2,3,3)(2,3,4)(2,4,4)(3,3,3)(3,3,4)(3,4,4)(4,4,4)
(2)只有a=2,b=3,c=4的一个三角形,如图所示的△ABC就是满足条件的三角形