题目内容
下列尺规作图,能判断AD是△ABC边上的高是( )
A. 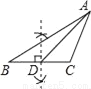 B.
B. 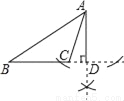 C.
C. 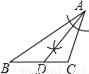 D.
D. 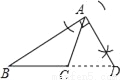
 B
【解析】试题分析:过点A作BC的垂线,垂足为D,故选B.
B
【解析】试题分析:过点A作BC的垂线,垂足为D,故选B.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
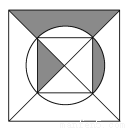
小学生10分钟应用题系列答案在如图所示的正方形纸片上做随机扎针实验,则针头扎在阴影区域内的概率为( )
A.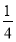 B.
B.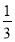
C.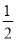 D.
D.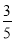
 A
【解析】根据正方形的性质易证正方形的对角线把正方形分成的四个三角形均为同底等高的三角形,故其面积相等,故阴影部分的面积占一份,故针头扎在阴影区域的概率为.
A
【解析】根据正方形的性质易证正方形的对角线把正方形分成的四个三角形均为同底等高的三角形,故其面积相等,故阴影部分的面积占一份,故针头扎在阴影区域的概率为. |2a-24|+(3a-b-k)2=0,那么k取什么值时,b为负数.
 k大于36时b为负数.
【解析】【试题分析】根据绝对值和完全平方的非负性,得 解得:a=12,b=36-k,当b<0时,即36-k<0,解得k>36.
【试题解析】
由题意得: 解得:b=36-k,
解得k>36.
故答案为k>36.
k大于36时b为负数.
【解析】【试题分析】根据绝对值和完全平方的非负性,得 解得:a=12,b=36-k,当b<0时,即36-k<0,解得k>36.
【试题解析】
由题意得: 解得:b=36-k,
解得k>36.
故答案为k>36. 不等式2x<6的非负整数解为( )
A.0,1,2 B.1,2 C.0,-1,-2 D.无数个
 A
【解析】
试题分析:先根据不等式的基本性质求得不等式的解集,即可得到结果.
由2x<6得x<3,非负整数解为0,1,2
故选A.
A
【解析】
试题分析:先根据不等式的基本性质求得不等式的解集,即可得到结果.
由2x<6得x<3,非负整数解为0,1,2
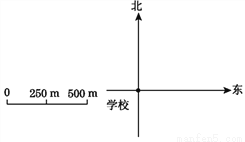
故选A. 市政建筑公司要在学校东面分别建造一座桥和一个汽车站(汽车站在学校的正东方向),桥在汽车站北面,现已知学校到桥、桥到汽车站及学校到汽车站的距离分别为500 m,500 m,250 m,请根据以上信息确定桥与汽车站应分别建在何处,在下面图纸上标出来(不写作法,保留作图痕迹);这三个场所构成一个什么形状的三角形?
 见解析
【解析】【试题分析】根据单位长度,画出图形即可.
【试题解析】
如图,A为汽车站的位置,B为桥的位置,这三个场所构成一个等腰三角形.
见解析
【解析】【试题分析】根据单位长度,画出图形即可.
【试题解析】
如图,A为汽车站的位置,B为桥的位置,这三个场所构成一个等腰三角形. 利用尺规作三角形,有三种基本类型:
(1)已知三角形的两边及其夹角,求作符合要求的三角形,其作图依据是“____”;
(2)已知三角形的两角及其夹边,求作符合要求的三角形,其作图依据是“____”;
(3)已知三角形的三边,求作符合要求的三角形,其作图依据是“____”.
 SAS ASA SSS
【解析】根据SAS—两边及其夹角分别相等的两个三角形全等;ASA—两角及其夹边分别相等的两个三角形全等;SSS—三边分别相等的两个三角形全等.
故答案:(1)SAS、 (2)ASA 、(3)SSS.
SAS ASA SSS
【解析】根据SAS—两边及其夹角分别相等的两个三角形全等;ASA—两角及其夹边分别相等的两个三角形全等;SSS—三边分别相等的两个三角形全等.
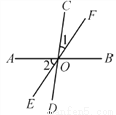
故答案:(1)SAS、 (2)ASA 、(3)SSS. 如图所示,AB,CD,EF交于点O,∠1=20°,∠2=60°,求∠BOC的度数.
 ∠BOC=80°.
【解析】试题分析:根据∠2和∠BOF是对顶角,所以∠2=∠BOF,所以∠BOC=∠1+∠BOF=20°+60°=80°.
试题解析:因为∠BOF=∠2=60°,
所以∠BOC=∠1+∠BOF=20°+60°=80°.
∠BOC=80°.
【解析】试题分析:根据∠2和∠BOF是对顶角,所以∠2=∠BOF,所以∠BOC=∠1+∠BOF=20°+60°=80°.
试题解析:因为∠BOF=∠2=60°,
所以∠BOC=∠1+∠BOF=20°+60°=80°. 如图(1)将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于E,AD平分∠BAC.
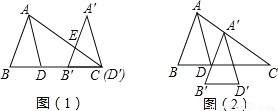
(1)猜想∠B′EC与∠A′之间的关系,并写出理由.
(2)如图将△ABD平移至如图(2)所示,得到△A′B′D′,请问:A′D平分∠B′A′C吗?为什么?
 (1)∠B′EC=2∠A′;(2)A′D′平分∠B′A′C.见解析
【解析】
试题分析:(1)根据平移的性质得出∠BAD=∠DAC,∠BAD=∠A′,AB∥A′B′,进而得出∠BAC=∠B′EC,进而得出答案;
(2)利用平移的性质得出∠B′A′D′=∠BAD,AB∥A′B′,进而得出∠BAD=∠BAC,即可得出∠B′A′D′=∠B′A′C.
【解析】
(1)∠B′EC=...
(1)∠B′EC=2∠A′;(2)A′D′平分∠B′A′C.见解析
【解析】
试题分析:(1)根据平移的性质得出∠BAD=∠DAC,∠BAD=∠A′,AB∥A′B′,进而得出∠BAC=∠B′EC,进而得出答案;
(2)利用平移的性质得出∠B′A′D′=∠BAD,AB∥A′B′,进而得出∠BAD=∠BAC,即可得出∠B′A′D′=∠B′A′C.
【解析】
(1)∠B′EC=... 在一次实验中,小明把一根弹簧的上端固定、在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体质量x的一组对应值.
所挂物体质量x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧长度y/cm | 18 | 20 | 22 | 24 | 26 | 28 |
①上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
②当所挂物体重量为3千克时,弹簧多长?不挂重物时呢?
③若所挂重物为7千克时(在允许范围内),你能说出此时的弹簧长度吗?
 ①上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;②当所挂物体重量为3千克时,弹簧长24厘米;当不挂重物时,弹簧长18厘米;③32厘米.
【解析】试题分析:①因为表中的数据主要涉及到弹簧的长度和所挂物体的质量,所以反映了所挂物体的质量和弹簧的长度之间的关系,所挂物体的质量是自变量;弹簧的长度是因变量;
②由表可知,当物体的质量为3kg时,弹簧的长...
①上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;②当所挂物体重量为3千克时,弹簧长24厘米;当不挂重物时,弹簧长18厘米;③32厘米.
【解析】试题分析:①因为表中的数据主要涉及到弹簧的长度和所挂物体的质量,所以反映了所挂物体的质量和弹簧的长度之间的关系,所挂物体的质量是自变量;弹簧的长度是因变量;
②由表可知,当物体的质量为3kg时,弹簧的长... 
