题目内容
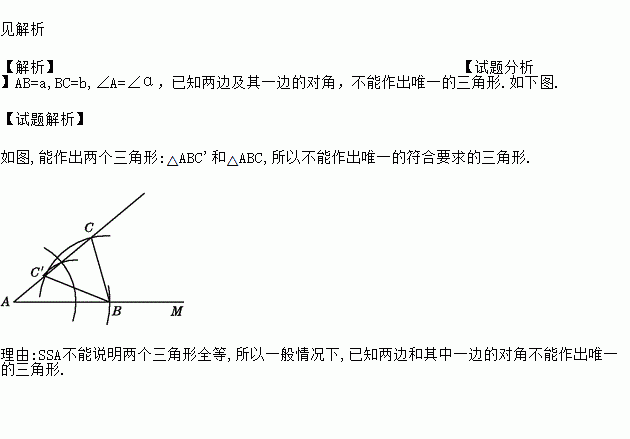
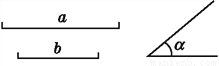
如图,已知线段a,b和∠α=40°,你能作出符合如下要求的唯一三角形吗?AB=a,BC=b,∠A=∠α,若能,写出作法;若不能,请说明理由.
见解析
【解析】【试题分析】AB=a,BC=b,∠A=∠α，已知两边及其一边的对角，不能作出唯一的三角形.如下图.
【试题解析】
如图,能作出两个三角形:△ABC'和△ABC,所以不能作出唯一的符合要求的三角形.
理由:SSA不能说明两个三角形全等,所以一般情况下,已知两边和其中一边的对角不能作出唯一的三角形.
练习册系列答案
字词句段篇系列答案
相关题目
如图,在4×4正方形网格中,任意选取一个白色的小正方形并涂上阴影,使图中阴影部分的图形构成一个轴对称图形的概率是( )
A. 
B. 
C. 
D.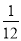 
A
【解析】【解析】
∵白色的小正方形有12个，能构成一个轴对称图形的有2个情况，∴使图中红色部分的图形构成一个轴对称图形的概率是： =．故选A． 要使不等式－3x－a≤0的解集为x≥1，那么a应满足什么条件？
a=－3
【解析】【试题分析】解不等式－3x－a≤0，得 又因为不等式的解集为x≥1，则 解得a=-3.
【试题解析】 －3x－a≤0，
又它的解集为x≥1，
故答案是a=-3. 下列四种说法：① x＝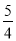
是不等式4x－5＞0的解；② x＝
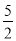是不等式4x－5＞0的一个解；③ x＞
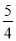是不等式4x－5＞0的解集；④ x＞2中任何一个数都可以使不等式4x－5＞0成立，所以x＞2也是它的解集，其中正确的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】①当 x＝时，不等式4x－5=0，故原命题错误；② 当x＝时，不等式4x－5=5＞0，故原命题正确；③解不等式4x－5＞0得，x＞，故原命题正确；④ 与③矛盾，故错误.故正确的有②和③，故选B. “综合与实践”学习活动准备制作一组三角形，记这些三角形的三边分别为a，b，c，并且这些三角形三边的长度为大于1且小于5的整数个单位长度．
（1）用记号（a，b，c）（a≤b≤c）表示一个满足条件的三角形，如（2，3，3）表示边长分别为2，3，3个单位长度的一个三角形．请列举出所有满足条件的三角形．
（2）用直尺和圆规作出三边满足a＜b＜c的三角形（用给定的单位长度，不写作法，保留作图痕迹）．
（1）答案见解析；（2）作图见解析.
【解析】试题分析：根据三角形的三边关系得出所有的结果；根据三角形的画法画出三角形．
试题解析：（1）共九种：（2,2,2）（2,2,3）（2,3,3）（2,3,4）（2,4,4）（3,3,3）（3,3,4）（3,4,4）（4,4,4）
（2）只有a=2，b=3，c=4的一个三角形，如图所示的△ABC就是满足条件的三角形 已知三边作三角形,用到的基本作图是( )
A. 作一个角等于已知角 B. 作已知直线的垂线
C. 作一条线段等于已知线段 D. 作一条线段等于已知线段的和
C
【解析】已知三角形的三边,求作符合要求的三角形,其作图依据是“SSS”.故用到的基本作图是：作一条线段等于已知线段.
故选C. 如图所示，直线AB与CD相交于点O，OE平分∠AOD，∠BOC=80°，求∠BOD和∠AOE的度数.
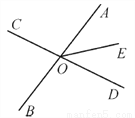
∠AOE=40°.
【解析】试题分析: 根据∠BOD与∠BOC是邻补角,∠BOC=80°,可求得:∠BOD=180°—∠BOC=100°,再根据∠AOD与∠BOC是对顶角,可得:∠AOD=∠BOC=80°,因为OE平分∠AOD,所以∠AOE=∠BOC=40°.
试题解析:因为∠BOD与∠BOC是邻补角,∠BOC=80°,
所以∠BOD=180°—∠BOC=100°,
又因为... 如图，直线AB和CD相交于点O，则∠AOC的邻补角是__________.
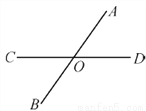
∠AOD和∠BOC
【解析】因为AB和CD交于点O,则∠AOC的邻补角是∠AOD和∠BOC,故答案为: ∠AOD和∠BOC. 如图，点C，F，E，B在一条直线上，∠CFD＝∠BEA，CE＝BF，DF＝AE，写出CD与AB之间的关系，并证明你的结论．
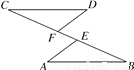
CD∥AB，CD＝AB，证明见解析.
【解析】试题分析:根据CE＝BF,可求证CF=BE,再根据∠CFD＝∠BEA,DF＝AE,
可证△DFC≌△AEB,利用全等三角形的性质可得: CD＝AB,∠C＝∠B,根据平行线的判定可证CD∥AB.
CD∥AB，CD＝AB，
证明如下：∵CE＝BF，∴CE－EF＝BF－EF，∴CF＝BE.
在△DFC和△AEB中，∴△DFC≌△...