先化简，再求值：（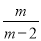
–
）÷
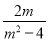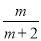，请在2，–2，0，3当中选一个合适的数代入求值．
,当m=3时，原式=3．
【解析】试题分析：括号内分式通分后相减，再把除法转化为乘法，分母分解因式后约分，然后再从给出的四个数中选择能使原分式有意义的值代入计算即可．
试题解析：
【解析】
原式＝
＝
＝，
当m＝3时，
原式＝＝3． 一个三角形的两边长为2和6，第三边为偶数．则这个三角形的周长为 ( )
A. 10 B. 12 C. 14 D. 16
C
【解析】试题解析：根据三角形的三边关系，得
6-2＜x＜6+2，
即4＜x＜8．
又∵第三边长是偶数，则x=6．
∴三角形的周长是2+6+6=14；
则该三角形的周长是14．
故选C. 在△ABC中，AB=4a，BC=14，AC=3a．则a的取值范围是 ( )
A. a＞2 B. 2＜a＜14 C. 7＜a＜14 D. a＜14
B
【解析】试题解析：∵△ABC中，AB=4a，BC=14，AC=3a，
∴解得2一个三角形的三个内角中，锐角的个数最少为 ( )]
A. 0 B. 1 C. 2 D. 3
C
【解析】试题解析：假设在一个三角形中只有1个锐角或一个锐角都没有,则另外的两个角或三个角都大于或等于
于是可得这个三角形的内角和大于
这样违背了三角形的内角和定理，假设不成立，
所以任何一个三角形的三个内角中至少有2个锐角.
故选C. 下面说法错误的是 ( )
A. 三角形的三条角平分线交于一点 B. 三角形的三条中线交于一点
C. 三角形的三条高交于一点 D. 三角形的三条高所在的直线交于一点
C
【解析】A. 三角形的三条角平分线交于一点，是三角形的内心，故命题正确；
B. 三角形的三条中线交于一点，是三角形的重心，故命题正确；
三角形的三条高所在的直线交于一点，三条高不一定相交，故C错误，D正确。
故选C. 能将一个三角形分成面积相等的两个三角形的一条线段是 ( )
A. 中线 B. 角平分线 C. 高线 D. 三角形的角平分线
A
【解析】试题解析：∵三角形的中线把三角形分成的两个三角形，底边相等，高是同一条高，
∴分成的两三角形的面积相等.
故选A. 如图，已知∠ACB=90°，CD⊥AB，垂足是D，则图中与∠A相等的角是 ( )
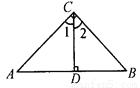
A. ∠1 B. ∠2 C. ∠B D. ∠1、∠2和∠B
B
【解析】试题解析：
∵∠ACB=即∠1+∠2=
又∵中,∠A+∠1=
∴∠A=∠2.
故选B. 点P是△ABC内任意一点，则∠APC与∠B的大小关系是 ( )
A. ∠APC＞∠B B. ∠APC=∠B C. ∠APC＜∠B D. 不能确定
A
【解析】试题解析：
如图，延长AP与BC相交于点D，
由三角形的外角性质得，∠PDC>∠B，∠APC>∠PDC，
所以，∠APC>∠B.
故选A. 已知：a、b、c是△ABC三边长，且M=(a＋b＋c)(a＋b－c)(a－b－c)，那么 ( )
A. M＞0 B. M=0 C. M＜0 D. 不能确定
C
【解析】试题解析：∵a、b、c是△ABC三边长，
∴a+b+c>0，a+b?c>0，a?b?c<0，
∴M=(a+b+c)(a+b?c)(a?b?c)<0.
故选C. 周长为P的三角形中，最长边m的取值范围是 ( )
A. 
B. 
C. 
D. 
A
【解析】试题解析：三边相等时,
三边不相等时,最长边
所以,
故选A.