题目内容
一个三角形的两边长为2和6,第三边为偶数.则这个三角形的周长为 ( )
A. 10 B. 12 C. 14 D. 16
 C
【解析】试题解析:根据三角形的三边关系,得
6-2<x<6+2,
即4<x<8.
又∵第三边长是偶数,则x=6.
∴三角形的周长是2+6+6=14;
则该三角形的周长是14.
故选C.
C
【解析】试题解析:根据三角形的三边关系,得
6-2<x<6+2,
即4<x<8.
又∵第三边长是偶数,则x=6.
∴三角形的周长是2+6+6=14;
则该三角形的周长是14.
故选C.
练习册系列答案
相关题目
函数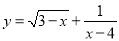 中.自变量x的取值范围是_____.
中.自变量x的取值范围是_____.
 x≤3
【解析】试题解析:根据题意得, 且x?4≠0,
解得.
故答案为:
x≤3
【解析】试题解析:根据题意得, 且x?4≠0,
解得.
故答案为: △ABC中,三个内角的度数均为整数,且∠A<∠B<∠C,4∠C=7∠A,求∠A的度数.
 44°
【解析】试题分析:先用∠A表示出∠C,再根据三角形的内角和等于180°列式整理用
∠A表示出∠B,再根据不等式求出∠A的取值范围,最后根据∠A是整数解答.
试题解析:
∵4∠C=7∠A,
∵∠A<∠B<∠C,
由①得,
由②得,
∵∠A,∠C是整数,
∴∠A是4的整数倍,
44°
【解析】试题分析:先用∠A表示出∠C,再根据三角形的内角和等于180°列式整理用
∠A表示出∠B,再根据不等式求出∠A的取值范围,最后根据∠A是整数解答.
试题解析:
∵4∠C=7∠A,
∵∠A<∠B<∠C,
由①得,
由②得,
∵∠A,∠C是整数,
∴∠A是4的整数倍, 一个三角形的三个内角的度数的比是2:2:1,这个三角形是_________三角形.
 锐角(等腰锐角)
【解析】试题解析:一个三角形的三个内角的度数的比是2:2:1,则一定有两个角相等,则三角形是:等腰三角形,
底角一定大于顶角,则三角形一定是锐角三角形.
故答案是:锐角(等腰锐角).
锐角(等腰锐角)
【解析】试题解析:一个三角形的三个内角的度数的比是2:2:1,则一定有两个角相等,则三角形是:等腰三角形,
底角一定大于顶角,则三角形一定是锐角三角形.
故答案是:锐角(等腰锐角). 如图,已知∠ACB=90°,CD⊥AB,垂足是D,则图中与∠A相等的角是 ( )
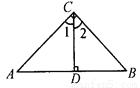
A. ∠1 B. ∠2 C. ∠B D. ∠1、∠2和∠B
 B
【解析】试题解析:
∵∠ACB=即∠1+∠2=
又∵中,∠A+∠1=
∴∠A=∠2.
故选B.
B
【解析】试题解析:
∵∠ACB=即∠1+∠2=
又∵中,∠A+∠1=
∴∠A=∠2.
故选B. 若代数式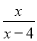 有意义,则实数
有意义,则实数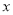 的取值范围是( )
的取值范围是( )
A. x=0 B. x=4 C. x≠0 D. x≠4
 D
【解析】由分式有意义的条件:分母不为0,即x-4≠0,解得x≠4,
故选D.
D
【解析】由分式有意义的条件:分母不为0,即x-4≠0,解得x≠4,
故选D. 下列分式是最简分式的是( )
A. 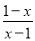 B.
B. 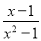
C. 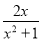 D.
D. 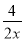
 C
【解析】根据最简分式的特点,分子分母没有公因式,因此A可化为,不是最简分式;B可化为,不是最简分式;C是最简分式;D可化简为,不是最简分式.
故选:C.
C
【解析】根据最简分式的特点,分子分母没有公因式,因此A可化为,不是最简分式;B可化为,不是最简分式;C是最简分式;D可化简为,不是最简分式.
故选:C. 如图,在Rt△ABC中,∠C=90°,AB=2BC,则sinB的值为 .
 【解析】试题分析:因为在Rt△ABC中,∠C = 90°,AB = 2BC,所以.
【解析】试题分析:因为在Rt△ABC中,∠C = 90°,AB = 2BC,所以. 某移动通信公司开设了两种通信业务,“全球通”:使用时首先缴50元月租费,然后每通话1分钟,付话费0.4元;“动感地带”:不缴月租费,每通话1分钟,付话费0.6元(本题的通话均指市内通话).若一个月通话x分钟,两种方式的费用分别为y1元和y2元.
(1)写出y1,y2与x之间的关系式;
(2)一个月内通话多少分钟,两种方式费用相同?
(3)某人估计一个月内通话300分钟,应选择哪种方式更合算些?
 【解析】
(1)y1=50+0.4x,y2=0.6x (2)当每个月通话250分钟时,两种方式费用相同 (3)使用“全球通”合算
【解析】试题分析:(1)理解每种通信业务的付费方式,依据每分钟通话费用×通话时长便可确定每种方式的费用,进而写出y1、y2的关系式;
对于(2),令y1=y2,解方程即可;
对于(3),令x=300,分别求出y1、y2的值,再做比较即可.
【解...
【解析】
(1)y1=50+0.4x,y2=0.6x (2)当每个月通话250分钟时,两种方式费用相同 (3)使用“全球通”合算
【解析】试题分析:(1)理解每种通信业务的付费方式,依据每分钟通话费用×通话时长便可确定每种方式的费用,进而写出y1、y2的关系式;
对于(2),令y1=y2,解方程即可;
对于(3),令x=300,分别求出y1、y2的值,再做比较即可.
【解... 
