题目内容
一个三角形的三个内角中,锐角的个数最少为 ( )]
A. 0 B. 1 C. 2 D. 3
 C
【解析】试题解析:假设在一个三角形中只有1个锐角或一个锐角都没有,则另外的两个角或三个角都大于或等于
于是可得这个三角形的内角和大于
这样违背了三角形的内角和定理,假设不成立,
所以任何一个三角形的三个内角中至少有2个锐角.
故选C.
C
【解析】试题解析:假设在一个三角形中只有1个锐角或一个锐角都没有,则另外的两个角或三个角都大于或等于
于是可得这个三角形的内角和大于
这样违背了三角形的内角和定理,假设不成立,
所以任何一个三角形的三个内角中至少有2个锐角.
故选C.
练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
圆周长C与圆的半径r之间的关系为C=2πr,其中变量是________,________ ,常量是________ .
 c r 2π
【解析】在圆的周长公式C=2πr中,C与r是改变的,π是不变的,所以变量是C,r,常量是2π.
c r 2π
【解析】在圆的周长公式C=2πr中,C与r是改变的,π是不变的,所以变量是C,r,常量是2π. 如图,豫东有四个村庄A、B、C、D.现在要建造一个水塔P.请回答水塔P应建在何位置,才能使它到4村的距离之和最小,说明最节约材料的办法和理由.
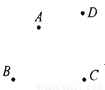
 说明见解析.
【解析】试题分析:根据线段的性质:两点之间,线段距离最短;结合题意,要使它与四个村庄的距离之和最小,就要使它在AC与BD的交点处.
试题解析:
如图,水塔P应建在线段AC和线段BD的交点P处。这样的设计将最节省材料.
理由:我们不妨任意取一点P′,连接AP′、BP、CP′、DP′、AB、BC、CD、DA,
∵△AP′C中,AP′+CP′>AC=AP+CP...
说明见解析.
【解析】试题分析:根据线段的性质:两点之间,线段距离最短;结合题意,要使它与四个村庄的距离之和最小,就要使它在AC与BD的交点处.
试题解析:
如图,水塔P应建在线段AC和线段BD的交点P处。这样的设计将最节省材料.
理由:我们不妨任意取一点P′,连接AP′、BP、CP′、DP′、AB、BC、CD、DA,
∵△AP′C中,AP′+CP′>AC=AP+CP... 已知:a、b、c是△ABC三边长,且M=(a+b+c)(a+b-c)(a-b-c),那么 ( )
A. M>0 B. M=0 C. M<0 D. 不能确定
 C
【解析】试题解析:∵a、b、c是△ABC三边长,
∴a+b+c>0,a+b?c>0,a?b?c<0,
∴M=(a+b+c)(a+b?c)(a?b?c)<0.
故选C.
C
【解析】试题解析:∵a、b、c是△ABC三边长,
∴a+b+c>0,a+b?c>0,a?b?c<0,
∴M=(a+b+c)(a+b?c)(a?b?c)<0.
故选C. 化简: 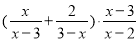 =____________.
=____________.
 1
【解析】根据分式的混合运算,先算括号里面的,再算乘法化简即可得===1.
故答案为:1.
1
【解析】根据分式的混合运算,先算括号里面的,再算乘法化简即可得===1.
故答案为:1. 下列运算正确的是( )
A. 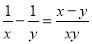 B.
B. 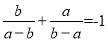
C. 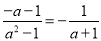 D.
D. 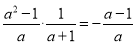
 B
【解析】根据分式的运算,可知:
A. =,故不正确;
B. =,故不正确;
C. =,故不正确;
D. =,故不正确.
故选:B.
B
【解析】根据分式的运算,可知:
A. =,故不正确;
B. =,故不正确;
C. =,故不正确;
D. =,故不正确.
故选:B. 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,求∠ABC的正弦值.
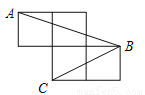
 ∠ABC的正弦值为
【解析】试题分析:首先利用勾股定理计算出AB2,BC2,AC2,再根据勾股定理逆定理可证明∠BCA=90°,然后得到∠ABC的度数,再利用特殊角的三角函数可得∠ABC的正弦值.
试题解析:连接
AB2=32+12=10,BC2=22+12=5,AC=22+12=5,
∴AC=CB,BC2+AC2=AB2,
∴∠BCA=90°,
∴∠ABC=4...
∠ABC的正弦值为
【解析】试题分析:首先利用勾股定理计算出AB2,BC2,AC2,再根据勾股定理逆定理可证明∠BCA=90°,然后得到∠ABC的度数,再利用特殊角的三角函数可得∠ABC的正弦值.
试题解析:连接
AB2=32+12=10,BC2=22+12=5,AC=22+12=5,
∴AC=CB,BC2+AC2=AB2,
∴∠BCA=90°,
∴∠ABC=4... (3分)在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )
A.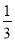 B.3 C.
B.3 C.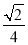 D.
D.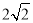
 D.
【解析】
试题分析:设BC=x,则AB=3x,由勾股定理得,AC=,tanB===,故选D.
D.
【解析】
试题分析:设BC=x,则AB=3x,由勾股定理得,AC=,tanB===,故选D. 
