题目内容
已知：a、b、c是△ABC三边长，且M=(a＋b＋c)(a＋b－c)(a－b－c)，那么 ( )
A. M＞0 B. M=0 C. M＜0 D. 不能确定
C
【解析】试题解析：∵a、b、c是△ABC三边长，
∴a+b+c>0，a+b?c>0，a?b?c<0，
∴M=(a+b+c)(a+b?c)(a?b?c)<0.
故选C.
练习册系列答案
相关题目
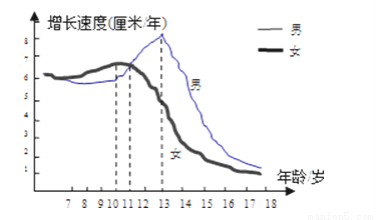
生物学研究表明，在8﹣﹣17岁期间，男女生身高增长速度规律呈现如下图所示，请你观察此图，回答下列问题，男生身高增长速度的巅峰是几岁？在几岁时男生、女生的身高增长速度是一样的？
见解析
【解析】试题分析：结合图形观察男生女生的增长线图的最高点即是身高增长速度的巅峰，两身高线的交点就是他们的增长速度一样．
试题解析：男生身高增长速度的巅峰是13岁，在11岁时男生、女生身高增长速度是一样的。 已知点A的坐标为（-2，3），点B的坐标为（0，1），则点A关于点B的坐标为（ ）
A. （ -2，2 ） B. （2，-3 ） C. （ 2，-1 ） D. （2，3 ）
C
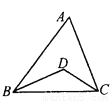
【解析】因为点A的坐标为（-2,3）,点B的坐标为（0,1）,则点A关于点B的坐标为（2,-1）,故选C. 如图，△ABC中，∠A=60°，∠ABC、∠ACB的平分线BD、CD交于点D，则∠BDC=_____．
120°
【解析】试题解析：在△ABC中，
∵BD是∠ABC的平分线，CD是∠ACB的平分线，
在△BCI中，
故答案为： 一个三角形的三个内角的度数的比是2：2：1，这个三角形是_________三角形．
锐角（等腰锐角）
【解析】试题解析：一个三角形的三个内角的度数的比是2:2:1，则一定有两个角相等，则三角形是：等腰三角形，
底角一定大于顶角，则三角形一定是锐角三角形.
故答案是：锐角(等腰锐角). 一个三角形的三个内角中，锐角的个数最少为 ( )]
A. 0 B. 1 C. 2 D. 3
C
【解析】试题解析：假设在一个三角形中只有1个锐角或一个锐角都没有,则另外的两个角或三个角都大于或等于
于是可得这个三角形的内角和大于
这样违背了三角形的内角和定理，假设不成立，
所以任何一个三角形的三个内角中至少有2个锐角.
故选C. 若代数式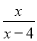
有意义，则实数
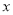的取值范围是（ ）
A. x=0 B. x=4 C. x≠0 D. x≠4
D
【解析】由分式有意义的条件:分母不为0，即x-4≠0，解得x≠4，
故选D. 如图所示，在3×3的正方形网格中已有两个小正方形被涂黑，再将图中其余小正方形任意涂黑一个，使整个图案构成一个轴对称图形的办法有
A．3种 B．4种 C．5种 D．6种
C
【解析】
试题分析：如果一个图形沿一条直线对折，直线两旁的部分能互相重合，那么这个图形叫做轴对称图形．
选择一个正方形涂黑，使得3个涂黑的正方形组成轴对称图形，
选择的位置有以下几种：1处，3处，7处，6处，5处，选择的位置共有5处
故选C. △ABC中，a、b、c分别是∠A、∠B、∠C的对边，如果a2+b2=c2，那么下列结论正确的是（ ）
A. bcosB=c B. csinA=a C. atanA=b D. tan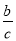B＝
B
【解析】∵a2+b2=c2，
∴△ABC是直角三角形，且∠C=90°，
∴sinA=即csinA=a，
∴B选项正确．
故选B．