题目内容
先化简,再求值:(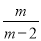 –
–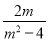 )÷
)÷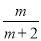 ,请在2,–2,0,3当中选一个合适的数代入求值.
,请在2,–2,0,3当中选一个合适的数代入求值.
 ,当m=3时,原式=3.
【解析】试题分析:括号内分式通分后相减,再把除法转化为乘法,分母分解因式后约分,然后再从给出的四个数中选择能使原分式有意义的值代入计算即可.
试题解析:
【解析】
原式=
=
=,
当m=3时,
原式==3.
,当m=3时,原式=3.
【解析】试题分析:括号内分式通分后相减,再把除法转化为乘法,分母分解因式后约分,然后再从给出的四个数中选择能使原分式有意义的值代入计算即可.
试题解析:
【解析】
原式=
=
=,
当m=3时,
原式==3.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案笔记本每本a元,买3本笔记本共支出y元,在这个问题中:
①a是常量时,y是变量;
②a是变量时,y是常量;
③a是变量时,y也是变量;
④a,y可以都是常量或都是变量;
上述判断正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
 B
【解析】由题意得:y=3a,
此问题中a、y都是变量,3是常量,或a,y都是常量,则③④,
故选:B.
B
【解析】由题意得:y=3a,
此问题中a、y都是变量,3是常量,或a,y都是常量,则③④,
故选:B. 已知:如图,P是△ABC内任一点,求证:∠BPC>∠A.
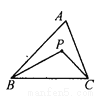
 说明见解析.
【解析】试题分析:延长BP交AC于D. 根据△PDC外角的性质知∠BPC>∠PDC,根据△ABD外角的性质知∠PDC>∠A,所以易证∠BPC>∠A.
试题解析:如图,延长BP交AC于D.
∵∠BPC>∠PDC,∠PDC>∠A,
∴∠BPC>∠A.
说明见解析.
【解析】试题分析:延长BP交AC于D. 根据△PDC外角的性质知∠BPC>∠PDC,根据△ABD外角的性质知∠PDC>∠A,所以易证∠BPC>∠A.
试题解析:如图,延长BP交AC于D.
∵∠BPC>∠PDC,∠PDC>∠A,
∴∠BPC>∠A. 能将一个三角形分成面积相等的两个三角形的一条线段是 ( )
A. 中线 B. 角平分线 C. 高线 D. 三角形的角平分线
 A
【解析】试题解析:∵三角形的中线把三角形分成的两个三角形,底边相等,高是同一条高,
∴分成的两三角形的面积相等.
故选A.
A
【解析】试题解析:∵三角形的中线把三角形分成的两个三角形,底边相等,高是同一条高,
∴分成的两三角形的面积相等.
故选A. 我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则;等等.小学里,把分子比分母小的分数叫做真分数.类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.任何一个假分式都可以化成整式与真分式的和的形式,如: 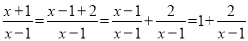 ;
; 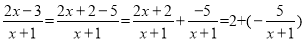
(1)下列分式中,属于真分式的是:________(填序号);
①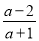 ②
②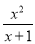 ③
③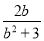 ④
④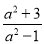
(2)将假分式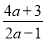 化成整式与真分式的和的形式:
化成整式与真分式的和的形式: 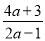 =________+________;
=________+________;
(3)将假分式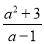 化成整式与真分式的和的形式:
化成整式与真分式的和的形式: 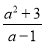 =__________________.
=__________________.
 (1)③;(2)2, ;(3)a+1+ .
【解析】试题分析:(1)认真阅读题意,体会真分式的特点,然后判断即可;
(2)根据题意的化简方法进行化简即可;
(3)根据题意的化简方法进行化简即可.
试题解析:(1)①中的分子分母均为1次,②中分子次数大于分母次数,③分子次数小于分母次数,④分子分母次数一样,故选③.
(2)=,故答案为:2, ;
(3)== ,故答...
(1)③;(2)2, ;(3)a+1+ .
【解析】试题分析:(1)认真阅读题意,体会真分式的特点,然后判断即可;
(2)根据题意的化简方法进行化简即可;
(3)根据题意的化简方法进行化简即可.
试题解析:(1)①中的分子分母均为1次,②中分子次数大于分母次数,③分子次数小于分母次数,④分子分母次数一样,故选③.
(2)=,故答案为:2, ;
(3)== ,故答... 已知分式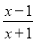 的值是零,那么x的值是( )
的值是零,那么x的值是( )
A. -1 B. 0
C. 1 D. ±1
 C
【解析】由题意得:x-1=0,则x=1,故选C.
C
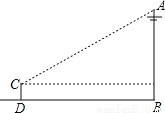
【解析】由题意得:x-1=0,则x=1,故选C. 如图,为了测量电线杆AB的高度,小明将测量仪放在与电线杆的水平距离为9m的D处.若测角仪CD的高度为1.5m,在C处测得电线杆顶端A的仰角为36°,则电线杆AB的高度约为____(精确到0.1m).(参考数据sin36°≈0.59.cos36°≈0.81,tan36°≈0.73).
 8.1 m.
【解析】如图作CE⊥AB,垂足为E.
∵=tan 36°,
CE=BD,
∴AE=BD·tan 36°
≈9×0.73
=6.57,
∴AB=6.57+1.5=8.07≈8.1.
8.1 m.
【解析】如图作CE⊥AB,垂足为E.
∵=tan 36°,
CE=BD,
∴AE=BD·tan 36°
≈9×0.73
=6.57,
∴AB=6.57+1.5=8.07≈8.1. 小明某天上午9时骑自行车离开家,15时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).
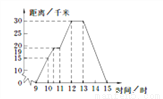
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
 (1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)11千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
【解析】解:(1)图象表示了时间、距离的关系,自变量是时间,因变量是距离. (2)由图象看出10时他距家15千米,13时他距家30千米. (3)由图象看...
(1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)11千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
【解析】解:(1)图象表示了时间、距离的关系,自变量是时间,因变量是距离. (2)由图象看出10时他距家15千米,13时他距家30千米. (3)由图象看... 
