下列语句中，正确的是（ ）
A. 有一条公共边且和为180°的两个角是邻角；
B. 互为邻补角的两个角不相等；
C. 两边互为反向延长线的两个角是对顶角；
D. 交于一点的三条直线形成3对对顶角。
C
【解析】试题分析：A、邻角的度数之和不一定要180°，故错误；B、当两个邻补角都是90°时则两个角相等，故错误；C、正确；D、交于一点的三条直线形成5对对顶角，故错误，故本题选C． 如图，如果AD∥BC，则有
①∠A+∠B=180°；②∠B+∠C=180°；③∠C+∠D=180°，上述结论中正确的是（ ）
A. 只有①； B. 只有②； C. 只有③； D. 只有①和③
D
【解析】试题分析：根据两直线平行，同旁内角互补可得：∠A+∠B=180°，∠C+∠D=180°，则本题选D． 如图，如果AB∥CD，CD∥EF，那么∠BCE等于（ ）
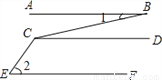
A. ∠1＋∠2 B. ∠2－∠1 C. 180°－∠2＋∠1 D. 180°－∠1＋∠2
C
【解析】试题分析：根据AB∥CD可得：∠BCD=∠1；根据CD∥EF可得：∠2+∠DCE=180°，则∠DCE=180°-∠2，则∠BCE=∠BCD+∠DCE=∠1+180°-∠2，故选C． 如果直线a∥b，b∥c，那么a∥c。这个推理的依据是（ ）
A. 等量代换； B. 平行公理；
C. 两直线平行，同位角相等； D. 平行于同一直线的两条直线平行。
D
【解析】试题分析：在同一平面内，平行于同一条直线的两直线平行，故本题选D． 如图，∠3与∠B是直线AB、______被直线______所截而成的______角；∠1与∠A是直线AB、______被直线______所截而成的______角；∠2与∠A是直线AB、______被直线______所截而成的______角。
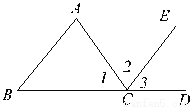
（1）CE，BD，同位；BD，AC，同旁内；CE，AC，内错。
【解析】试题分析：如图，∠3与∠B是直线AB、CE被直线BD所截而成的同为角；∠1与∠A是直线AB、BD被直线AC所截而成的同旁内角；∠2与∠A是直线AB、CE被直线AC所截而成的内错角． 已知：如图，AB∥CD，EF分别交于AB、CD于E、F，EG平分∠AEF，FH平分∠EFD。
求证： EG∥FH
证明：∵ AB∥CD（已知），∴ ∠AEF=∠EFD （______）。∵ EG平分∠AEF，FH平分∠EFD（______），∴∠______=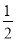
∠AEF，∠______=
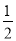∠EFD（角平分线定义）。∴ ∠______=∠______，∴ EG∥FH（______）。
两直线平行，内错角相等，已知，∠GEF，∠EFH，∠GEF，∠EFH，内错角相等，两直线平行。
【解析】试题分析：本题只要根据平行线的性质以及角平分线的性质得出角相等，最后根据内错角相等，两直线平行得出答案． 已知：如图，∠1=35º，AB⊥CD，垂足为O，EF经过点O。求∠2、∠3、∠4的度数。
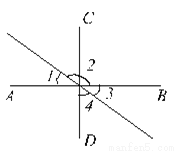
∠2=145°，∠3=35°， ∠4=55°
【解析】试题分析：首先根据对顶角的性质得出∠3的度数，根据邻补角的性质求出∠2的度数，最后根据垂直的定义求出∠4的度数．
试题解析：∵∠1和∠3是对顶角， ∴∠3=∠1=35°， ∵∠1+∠2=180°，
∴∠2=180°-∠1=180°-35°=145°， ∵AB⊥CD， ∴∠3+∠4=90°，
∴∠4=90°-∠3=90°-... 已知：如图，直线EF与AB、CD分别相交于点G、H，∠1=∠3。
求证：AB∥CD。
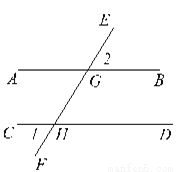
证明见解析
【解析】试题分析：首先根据对顶角的性质得出∠AGH=∠GHD，最后根据内错角相等两直线平行得出答案．
试题解析：∵∠1=∠GHD，∠3=∠AGH（对顶角相等），∠1=∠3（已知），∴∠AGH=∠GHD，
∴AB∥CD（内错角相等，内错角相等）． 已知：如图，AB∥CD，BE∥CF。
求证：∠1=∠4。
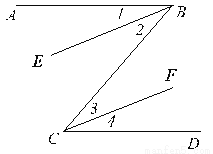
证明见解析
【解析】试题分析：根据AB∥CD得出∠ABC=∠BCD，然后根据BE∥CF得出∠2=∠3，从而得出答案．
试题解析：∵AB∥CD（已知）， ∴∠ABC=∠BCD（两条直线平行，内错角相等），
∵BE∥CF（已知），∴∠2=∠3（两条直线平行，内错角相等），
∵∠ABC=∠1+∠2，∠BCD=∠3+∠4，∴∠1=∠4． 已知：如图，BE∥DF，∠B=∠D。求证：AD∥BC。
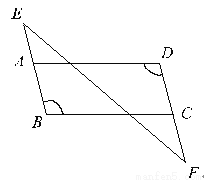
证明见解析
【解析】试题分析：根据BE∥DF得出∠D=∠EAD，结合已知条件得出∠B=∠EAD，从而根据同位角相等两直线平行得出答案．
试题解析：∵BE∥DF（已知），∴∠D=∠EAD（两条直线平行，内错角相等），
∵∠B=∠D（已知），∴∠B=∠EAD，∴AD∥BC（同位角相等，两直线平行）．