题目内容
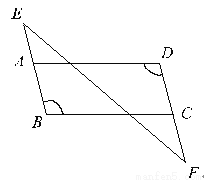
已知：如图，BE∥DF，∠B=∠D。求证：AD∥BC。
证明见解析
【解析】试题分析：根据BE∥DF得出∠D=∠EAD，结合已知条件得出∠B=∠EAD，从而根据同位角相等两直线平行得出答案．
试题解析：∵BE∥DF（已知），∴∠D=∠EAD（两条直线平行，内错角相等），
∵∠B=∠D（已知），∴∠B=∠EAD，∴AD∥BC（同位角相等，两直线平行）．
练习册系列答案
相关题目
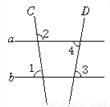
如图，∠1=82°，∠2=98°，∠3=80°,则∠4的度数为_____.
80°
【解析】
∵∠2=98°，
∴∠5=98°.
∵∠1=82°，
∴∠1+∠5=82°+98°=180°，
∴a∥b,
∵∠3=80°,
∴∠4=∠3=80°. 已知a＋b＝m，ab＝－4，化简(a－2)(b－2)的结果是( )
A. 6 B. 2m－8 C. 2m D. －2m
D
【解析】试题分析：因为（a﹣2）（b﹣2）="ab-2a-2b+4=" ab-2（a+b）+4，且a+b=m，ab=﹣4，所以原式=-4-2m+4=-2m，故选：D． 下列图形中，不是轴对称图形的是（ ）
A. 有两个内角相等的三角形 B. 有一个内角是45°直角三角形
C. 有一个内角是30°的直角三角形 D. 有两个角分别是30°和120°的三角形
C
【解析】试题分析：因为有两个内角相等的三角形是等腰三角形，是轴对称图形，所以A正确；因为有一个内角是45°直角三角形是等腰直角三角形，是轴对称图形，所以A正确；因为有一个内角是30°的直角三角形，不是轴对称图形，所以C错误；因为有两个角分别是30°和120°的三角形是等腰三角形，是轴对称图形，所以D正确；故选：C． 下列图形不确定是轴对称图形的是（ ）
A. 角 B. 线段 C. 直线 D. 三角形
D
【解析】【解析】
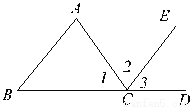
角、线段、直线都是轴对称图形；等腰三角形是轴对称图形，而一般的非等腰三角形不是轴对称图形．故选D． 如图，∠3与∠B是直线AB、______被直线______所截而成的______角；∠1与∠A是直线AB、______被直线______所截而成的______角；∠2与∠A是直线AB、______被直线______所截而成的______角。
（1）CE，BD，同位；BD，AC，同旁内；CE，AC，内错。
【解析】试题分析：如图，∠3与∠B是直线AB、CE被直线BD所截而成的同为角；∠1与∠A是直线AB、BD被直线AC所截而成的同旁内角；∠2与∠A是直线AB、CE被直线AC所截而成的内错角． 邻补角的角平分线所在的两条直线互相垂直。 （___）
√
【解析】试题分析：邻补角的角平分线所在的两条直线互相垂直，故本题答案为“√”． 笔记本每本a元，买3本笔记本共支出y元，在这个问题中：
①a是常量时，y是变量；
②a是变量时，y是常量；
③a是变量时，y也是变量；
④a，y可以都是常量或都是变量；
上述判断正确的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】由题意得：y=3a，
此问题中a、y都是变量，3是常量，或a，y都是常量，则③④，
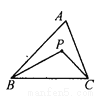
故选：B. 已知：如图，P是△ABC内任一点，求证：∠BPC＞∠A．
说明见解析.
【解析】试题分析：延长BP交AC于D. 根据△PDC外角的性质知∠BPC>∠PDC，根据△ABD外角的性质知∠PDC>∠A，所以易证∠BPC>∠A.
试题解析：如图，延长BP交AC于D.
∵∠BPC>∠PDC，∠PDC>∠A，
∴∠BPC>∠A.