如(x+m)与(x+3)的乘积中不含x的一次项，则m的值为 ( )
A. –3 B. 3 C. 0 D. 1
A
【解析】(x+m)(x+3)=x2+(3+m)x+3m,
因为结果不含x的一次项，所以3+m=0,m=-3,
故选A. 如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则长方形的面积为( )
A. (2a2+5a)cm2 B. (6a+15)cm2
C. (6a+9)cm2 D. (3a+15)cm2
B
【解析】由题意可得，(a+4)2-(a+1)2=a2+8a+16-(a2+2a+1)=a2+8a+16-a2-2a-1=6a+15(cm2)，故选B. 在下列计算中,不能用平方差公式计算的是( )
A. (m-n)(-m+n) B.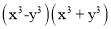 
C. (-a-b)(a-b) D.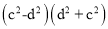 
A
【解析】运用平方差公式计算的两个多项式必须满足一项是相同，另一项互为相反数.选项B、C、D都符合要求，能用平方差公式计算；选项A中m和-m符号相反，n和-n符号相反，不符合要求，不能用平方差公式计算，故选A. 若9x2+kxy+16y2是完全平方式,则k的值为( )
A. 12 B. 24 C. ±12 D. ±24
D
【解析】已知9x2+kxy+16y2是完全平方式，可得kxy=±2×3x•4y，解得k=±24．故选D. 若A=(2+1)(22+1)(24+1)(28+1)+1,则A的末位数字是( )
A. 2 B. 4 C. 6 D. 8
C
【解析】试题分析：根据题意可得A=（2-1）（2+1）（22+1）（24+1）（28+1）
=（22-1）（22+1）（24+1）（28+1）
=（24-1）（24+1）（28+1）
=（28-1）（28+1）
=216-1
根据21=2；22=4；23=8；24=16；25=32；···因此可由16÷4=4，所以216的末位为6，则216-1的末位为5.
... 已知27m-1÷32m=27,则m=___________.
6
【解析】由题意知，(33)m-1÷32m=27.
所以33(m-1)-2m=33.
所以3m-3-2m=3，解得m=6. 若(3x+1)-3有意义,则x的取值范围是___________.
x≠-
【解析】(3x+1)-3= ，根据分式有意义的条件可得3x+1≠0，即. 计算:(-2)2 016+(-2)2 017=___________.
-22 016
【解析】 (-2)2 016+(-2)2 017=(-2)2 016(1-2)=-22 016. 计算:(0.125)2 018×(22 018)3=___________.
1
【解析】原式=(0.125)2 018×82 018=(0.125×8)2 018=1. 2(3+1)(32+1)(34+1)-38的值是___________.
-1
【解析】原式=(3-1)(3+1)(32+1)(34+1)-38
=(32-1)(32+1)(34+1)-38
=(34-1)(34+1)-38
=38-1-38
=-1.