题目内容
已知27m-1÷32m=27,则m=___________.
6
【解析】由题意知，(33)m-1÷32m=27.
所以33(m-1)-2m=33.
所以3m-3-2m=3，解得m=6.
练习册系列答案
相关题目
如图，矩形ABCD中，AB＝2AD，E为AD的中点，EF⊥EC交AB于点F，连接FC.
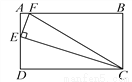
(1)求证：△AEF∽△DCE；
(2)求tan∠ECF的值．
（1）答案见解析；（2）
【解析】（1）根据矩形的性质可知∠A="∠D" =90°，再根据三角形的内角和为180°，可知∠DCE+∠DEC=900，由已知EF⊥EC，可得：∠AEF+∠DEC=900得出∠DCE=∠AEF，即可证明⊿AEF∽⊿DCE
（2）由（1）可知：⊿AEF∽⊿DCE ∴=
在矩形ABCD中，E为AD 的中点。
AB=2AD ∴ DC=AB=4AE ∴ ... 已知∠AOB=40°，OC平分∠AOB，则∠AOC的补角等于_____.
160°
【解析】
∵OC平分∠AOB，∠AOB=40°，
∴,
∴∠AOC的补角=180°-20°=160°. 已知(x2＋px＋8)(x2－3x＋q)的展开式中不含x2和x3项，求p，q的值．
p＝3，q＝1.
【解析】试题分析：根据整式的乘法，化简完成后，根据不含项的系数为0求解即可.
试题解析：∵（x2+px+8）（x2﹣3x+q）
=x4﹣3x3+qx2+px3﹣3px2+pqx+8x2﹣24x+8q
=x4+（p﹣3）x3+（q﹣3p+8）x2+（pq﹣24）x+8q．
∵乘积中不含x2与x3项，
∴p﹣3=0，q﹣3p+8=0，
∴p=... 已知x2-x-1=0,则代数式-x3+2x2+2 015的值为___________.
2016
【解析】由已知得x2-x=1，所以-x3+2x2+2 015=-x(x2-x)+x2+2 015=-x+x2+2 015=2 016. 如(x+m)与(x+3)的乘积中不含x的一次项，则m的值为 ( )
A. –3 B. 3 C. 0 D. 1
A
【解析】(x+m)(x+3)=x2+(3+m)x+3m,
因为结果不含x的一次项，所以3+m=0,m=-3,
故选A. 如图，已知点P是∠AOB平分线上一点，PC⊥OA，PD⊥OB，垂足为C，D.
(1)∠PCD＝∠PDC吗？为什么？
(2)OP是CD的垂直平分线吗？为什么？
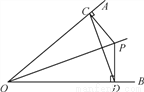
（1）见解析；（2）见解析
【解析】试题分析：（1）由角平分线的性质易得PC=PD，根据等边对等角即可得出∠PCD=∠PDC；
（2）易证△POC≌△POD，则OC=OD，根据线段垂直平分线的性质逆定理可得OP垂直平分CD．
试题解析：（1）∠PCD＝∠PDC，理由如下：
∵点P是∠AOB平分线上一点，PC⊥OA，PD⊥OB，
∴PC＝PD，
∴∠PCD＝∠PD... 下列图形中，轴对称图形有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
A
【解析】【解析】
给出的四个图形中，只有第一个是轴对称图形，其余虽然外形是，但是其内部图形不是，故选A． 汽车开始行驶时，油箱内有油40升，如果每小时耗油5升，则油箱内余油量Q（升）与行驶时间t（时）的关系用图象表示应为图中的是（ ）
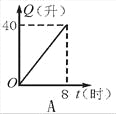
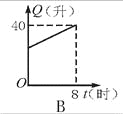
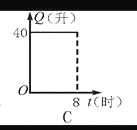
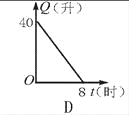
D
【解析】油箱内有油40升，那么余油量最初应是40，排除A. B；
随着时间的增多，余油量就随之减少，排除C.
正确的为D.
故选D.