题目内容
2(3+1)(32+1)(34+1)-38的值是___________.
 -1
【解析】原式=(3-1)(3+1)(32+1)(34+1)-38
=(32-1)(32+1)(34+1)-38
=(34-1)(34+1)-38
=38-1-38
=-1.
-1
【解析】原式=(3-1)(3+1)(32+1)(34+1)-38
=(32-1)(32+1)(34+1)-38
=(34-1)(34+1)-38
=38-1-38
=-1.
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
如图,在Rt△ABC中,∠C=90°,若sinA=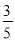 ,则cosB的是
,则cosB的是
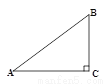
A. 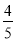 B.
B. 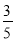 C.
C. 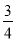 D.
D. 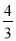
 B
【解析】试题分析:在Rt△ABC中,∵∠C=90°,
∴∠A+∠B=90°,
∴cosB=sinA,
∵sinA=,
∴cosB=.
故选:B.
B
【解析】试题分析:在Rt△ABC中,∵∠C=90°,
∴∠A+∠B=90°,
∴cosB=sinA,
∵sinA=,
∴cosB=.
故选:B. 如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE=_____.
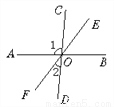
 53°
【解析】由∠BOE与∠AOF是对顶角,可得∠BOE=∠AOF,又因为∠COD是平角,可得∠1+∠2+∠AOF=180°,将∠1=95°,∠2=32°代入,即可求得∠AOF的度数,即∠BOE的度数.
53°
【解析】由∠BOE与∠AOF是对顶角,可得∠BOE=∠AOF,又因为∠COD是平角,可得∠1+∠2+∠AOF=180°,将∠1=95°,∠2=32°代入,即可求得∠AOF的度数,即∠BOE的度数. 如图是经过轴对称变换后所得的图形,与原图形相比
A.形状没有改变,大小没有改变 B.形状没有改变,大小有改变
C.形状有改变,大小没有改变 D.形状有改变,大小有改变
 A
【解析】
试题分析:∵轴对称变换不改变图形的形状与大小,
∴与原图形相比,形状没有改变,大小没有改变。
故选A。
A
【解析】
试题分析:∵轴对称变换不改变图形的形状与大小,
∴与原图形相比,形状没有改变,大小没有改变。
故选A。 先化简,再求值:-(a2-2ab)·9a2-(9ab3+12a4b2)÷3ab,其中a=-1,b=2.
 -49
【解析】试题分析:利用单项式乘以单项式的乘法法则和多项式除以单项式的除法法则计算后,合并同类项化为最简,再代入求值即可.
试题解析:
原式=-9a4+18a3b-3b2-4a3b=-9a4+14a3b-3b2.
将a=-1,b=2代入得,原式=-49.
-49
【解析】试题分析:利用单项式乘以单项式的乘法法则和多项式除以单项式的除法法则计算后,合并同类项化为最简,再代入求值即可.
试题解析:
原式=-9a4+18a3b-3b2-4a3b=-9a4+14a3b-3b2.
将a=-1,b=2代入得,原式=-49. 若A=(2+1)(22+1)(24+1)(28+1)+1,则A的末位数字是( )
A. 2 B. 4 C. 6 D. 8
 C
【解析】试题分析:根据题意可得A=(2-1)(2+1)(22+1)(24+1)(28+1)
=(22-1)(22+1)(24+1)(28+1)
=(24-1)(24+1)(28+1)
=(28-1)(28+1)
=216-1
根据21=2;22=4;23=8;24=16;25=32;···因此可由16÷4=4,所以216的末位为6,则216-1的末位为5.
...
C
【解析】试题分析:根据题意可得A=(2-1)(2+1)(22+1)(24+1)(28+1)
=(22-1)(22+1)(24+1)(28+1)
=(24-1)(24+1)(28+1)
=(28-1)(28+1)
=216-1
根据21=2;22=4;23=8;24=16;25=32;···因此可由16÷4=4,所以216的末位为6,则216-1的末位为5.
... 下列计算正确的是( )
A. -bx2y3÷2xy3=-3x B. (-xy2)2÷(-x2y)=-y3
C. (-2x2y2)3÷(-xy)3=-2x3y3 D. -(-a3b2)÷(-a2b2)=a4
 B
【解析】选项A,-bx2y3÷2xy3=-bx;选项B,原式==-y3;选项C,(-2x2y2)3÷(-xy)3=8x3y3;选项D,-(-a3b2)÷(-a2b2)=-a.故选B.
B
【解析】选项A,-bx2y3÷2xy3=-bx;选项B,原式==-y3;选项C,(-2x2y2)3÷(-xy)3=8x3y3;选项D,-(-a3b2)÷(-a2b2)=-a.故选B. 在等边△ABC中,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长为 ( )
A. 2a B. 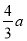 C. 1.5a D. a
C. 1.5a D. a
 C
【解析】【解析】
△ABC是等边三角形,由折叠可知,AD=BD=0.5AB=0.5a,易得△ADE是等边三角形.故周长是1.5a。故选 C.
C
【解析】【解析】
△ABC是等边三角形,由折叠可知,AD=BD=0.5AB=0.5a,易得△ADE是等边三角形.故周长是1.5a。故选 C. 如图,下图是汽车行驶速度(千米/时)和时间(分)的关系图,下列说法其中正确的个数为( )
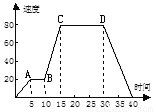
(1)汽车行驶时间为40分钟;(2)AB表示汽车匀速行驶;(3)在第30分钟时,汽车的速度是90千米/时;(4)第40分钟时,汽车停下来了.
A. 1个 B. 2个 C. 3个 D. 4个
 C
【解析】试题分析:仔细分析图象特征,根据横轴和纵轴的意义依次分析各小题即可作出判断.
【解析】
由图可得,在x=40时,速度为0,故(1)(3)正确;
AB段,y的值相等,故速度不变,故(2)正确;
x=30时,y=80,即在第30分钟时,汽车的速度是80千米/时;故(4)错误;
故选C.
C
【解析】试题分析:仔细分析图象特征,根据横轴和纵轴的意义依次分析各小题即可作出判断.
【解析】
由图可得,在x=40时,速度为0,故(1)(3)正确;
AB段,y的值相等,故速度不变,故(2)正确;
x=30时,y=80,即在第30分钟时,汽车的速度是80千米/时;故(4)错误;
故选C. 
