题目内容
计算:(-2)2 016+(-2)2 017=___________.
 -22 016
【解析】 (-2)2 016+(-2)2 017=(-2)2 016(1-2)=-22 016.
-22 016
【解析】 (-2)2 016+(-2)2 017=(-2)2 016(1-2)=-22 016.
练习册系列答案
相关题目
如图,直线y=2x+2与y轴交于A点,与反比例函数y=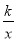 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
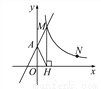
(1)求k的值;
(2)点N(a,1)是反比例函数y=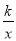 (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
 (1)4;(2)P(,0)
【解析】试题分析:(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标.从而可求K的值;
(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置.
(1)4;(2)P(,0)
【解析】试题分析:(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标.从而可求K的值;
(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置. 如图,已知直线a∥b,c∥d,∠1=115°,则∠2=_____,∠3=_____.
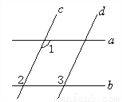
 115° 115°
【解析】∵a∥b,∠1=115°,
∴∠2=∠1=115°.
∵c∥d,
∴∠3=∠2=115°.
115° 115°
【解析】∵a∥b,∠1=115°,
∴∠2=∠1=115°.
∵c∥d,
∴∠3=∠2=115°. 计算: 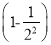 ×
×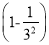 ×
×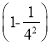 ×…×
×…×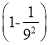 ×
×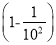 .
.
 【解析】试题分析:先把所给式子的每一个括号内的式子利用平方差公式因式分解,分别计算后约分即可.
试题解析:
原式=××××1+××…××
=××××××…××
=.
【解析】试题分析:先把所给式子的每一个括号内的式子利用平方差公式因式分解,分别计算后约分即可.
试题解析:
原式=××××1+××…××
=××××××…××
=. 已知a+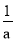 =5,则a2+
=5,则a2+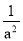 的结果是___________.
的结果是___________.
 23
【解析】由题意知=25,即a2++2=25,所以a2+=23.
23
【解析】由题意知=25,即a2++2=25,所以a2+=23. 在下列计算中,不能用平方差公式计算的是( )
A. (m-n)(-m+n) B. 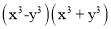
C. (-a-b)(a-b) D. 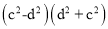
 A
【解析】运用平方差公式计算的两个多项式必须满足一项是相同,另一项互为相反数.选项B、C、D都符合要求,能用平方差公式计算;选项A中m和-m符号相反,n和-n符号相反,不符合要求,不能用平方差公式计算,故选A.
A
【解析】运用平方差公式计算的两个多项式必须满足一项是相同,另一项互为相反数.选项B、C、D都符合要求,能用平方差公式计算;选项A中m和-m符号相反,n和-n符号相反,不符合要求,不能用平方差公式计算,故选A. 下列运算正确的是( )
A. x2+x2=x4 B. (a-b)2=a2-b2 C. (-a2)3=-a6 D. 3a2·2a3=6a6
 C
【解析】试题分析:A、x2+x2=2x2,故错误;B、(a-b)2=a2-2ab+b2,故错误;C、(-a2)3=-a6,正确;D、3a2·2a3=6a5,故错误;
故选C.
C
【解析】试题分析:A、x2+x2=2x2,故错误;B、(a-b)2=a2-2ab+b2,故错误;C、(-a2)3=-a6,正确;D、3a2·2a3=6a5,故错误;
故选C. 下列图形中,线段AB和A’B’ (AB=A’B’)不关于直线l对称的是( )
A. 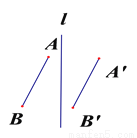 B.
B. 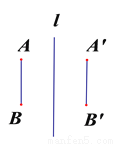 C.
C. 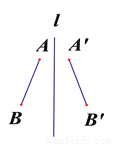 D.
D. 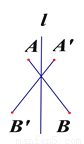
 A
【解析】【解析】
如果关于直线l对称,那么应该符合:对应点所连线段被对称轴垂直平分.由此可以判断出A不对称,故选A.
A
【解析】【解析】
如果关于直线l对称,那么应该符合:对应点所连线段被对称轴垂直平分.由此可以判断出A不对称,故选A. 某人先以v1的速度由A地出发去B地,途中在超市购买了一瓶水之后,又以v2的速度继续进行至B地,已知v1<v2 , 下面图象中能表示他从A地到B地的时间t(分钟)与路程s(千米)之间关系的是( )
A. 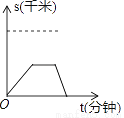 B.
B. 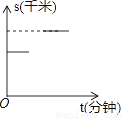
C. 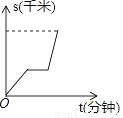 D.
D. 
 C
【解析】∵V1<V2,
∴题中图象上表示为开始时图象斜率小,后来斜率大,
又∵途中买了一瓶水,
∴图象有一段平行于x轴,
故选C.
C
【解析】∵V1<V2,
∴题中图象上表示为开始时图象斜率小,后来斜率大,
又∵途中买了一瓶水,
∴图象有一段平行于x轴,
故选C. 
