题目内容
若A=(2+1)(22+1)(24+1)(28+1)+1,则A的末位数字是( )
A. 2 B. 4 C. 6 D. 8
C
【解析】试题分析：根据题意可得A=（2-1）（2+1）（22+1）（24+1）（28+1）
=（22-1）（22+1）（24+1）（28+1）
=（24-1）（24+1）（28+1）
=（28-1）（28+1）
=216-1
根据21=2；22=4；23=8；24=16；25=32；···因此可由16÷4=4，所以216的末位为6，则216-1的末位为5.
...
如图，在△ABC中，CD⊥AB，垂足为点D.若AB＝12，CD＝6，tanA＝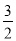
，求sinB＋cosB的值．
.
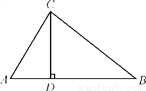
【解析】试题分析：先在Rt△ACD中，由正切函数的定义得tanA==，求出AD=4，则BD=AB﹣AD=8，再解Rt△BCD，由勾股定理得BC==10，sinB==，cosB==，由此求出sinB+cosB=．
【解析】
在Rt△ACD中，∵∠ADC=90°，
∴tanA===，
∴AD=4，
∴BD=AB﹣AD=12﹣4=8．
在Rt△BCD中，∵∠BD... 如图，直线AB、CD相交于点O，OB平分∠DOE，若∠DOE=60°，则∠AOC的度数是_____.
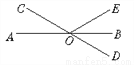
30°
【解析】因为∠BOD=45°，所以∠AOC=∠BOD=45°（对顶角相等），因为OE⊥AB，∴∠AOE=90°，所以∠COE=∠COA+∠AOE=45°+90°=135°. 先阅读再解答:我们已经知道,根据几何图形的面积关系可以说明完全平方公式,实际上还有一些等式也可以用这种方式加以说明,例如:
(2a+b)(a+b)=2a2+3ab+b2,就可以用图①的面积关系来说明.
(1)根据图②写出一个等式: ;
(2)已知等式:(x+p)(x+q)=x2+(p+q)x+pq,请你画出一个相应的几何图形加以说明.
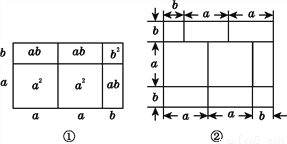
(1)(2a+b)(a+2b)=2a2+5ab+2b2(2)图形见解析
【解析】试题分析：（1）根据所给的长方形面积的两种表示法即可得等式；（2）画一个长为x+p，宽为x+q的长方形即可．
试题解析：
(1)(2a+b)(a+2b)=2a2+5ab+2b2
(2)如图.(所画图形不唯一) 2(3+1)(32+1)(34+1)-38的值是___________.
-1
【解析】原式=(3-1)(3+1)(32+1)(34+1)-38
=(32-1)(32+1)(34+1)-38
=(34-1)(34+1)-38
=38-1-38
=-1. 若3x=4，9y=7，则3x-2y的值为（ ）
A．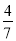
B．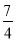
C．-3 D．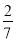
A
【解析】
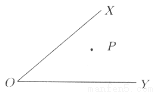
由3x=4，9y=7与3x-2y=3x÷32y=3x÷（32）y，代入即可求得答案． 如图，∠XOY内有一点P，试在射线OX上找出一点M，在射线OY上找出一点N，使PM+MN+NP最短.
见解析
【解析】【解析】
如图所示，分别以直线OX、OY为对称轴，作点P的对称点与，
连接，分别交OX于点M，交OY于点N，则PM+MN+NP最短． 对于下列命题：（1）关于某一直线成轴对称的两个三角形全等；（2）等腰三角形的对称轴是顶角的平分线；（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点；（4）如果两个三角形全等，那么它们关于某直线成轴对称。其中真命题的个数为
A、0 B、1 C、2 D、3
C
【解析】
试题分析：根据平面图形的基本概念依次分析各小题即可作出判断.
（1）关于某一直线成轴对称的两个三角形全等，（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点，均为真命题；
（2）等腰三角形的对称轴是顶角的平分线所在的直线，（4）如果两个三角形全等，它们可能是平移或旋转构成的，均为假命题；
故选C. 在动画片《喜羊羊与灰太狼》中，有一次灰太狼追赶喜羊羊，在距羊村40m处追上了喜羊羊．如图中s表示它们与羊村的距离（单位：m），t表示时间（单位：s）．根据相关信息判断，下列说法中错误的是（ ）
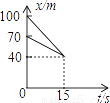
A. 喜羊羊与灰太狼最初的距离是30m B. 灰太狼用15s追上了喜羊羊
C. 灰太狼跑了60m追上了喜羊羊 D. 灰太狼追上喜羊羊时，喜羊羊跑了60m
D
【解析】观察图象可得，喜羊羊与灰太狼最初的距离是100-70=30m，选项A正确；由横坐标看出，15秒灰太狼追上了喜羊羊，选项B正确；由纵坐标看出，灰太狼跑了100-40=60米追上喜羊羊，选项C正确；由纵坐标看出，灰太狼追上喜羊羊时喜羊羊跑了70-40=30米，选项D错误；故选D．