探索:
(x-1)(x+1)=x2-1, (x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1, (x-1)(x4+x3+x2+x+1)=x5-1,
……
(1)试写出第五个等式;
(2)试求26+25+24+23+22+2+1的值;
(3)判断22 017+22 016+22 015+…+22+2+1的值的个位数字是几.
（1）x6-1（2）127（3）3
【解析】试题分析：(1)观察所给的四个等式，找出规律，写出第五个式子即可；（2）把26+25+24+23+22+2+1乘以（2-1），利用（1）所得的规律计算即可；（3）把22 017+22 016+22 015+…+22+2+1乘以（2-1），利用（1）所得的规律计算得到的结果为22 018-1，根据 （n≥1，且为整数）的末位数字4个一循环，由此计算出... 如图是经过轴对称变换后所得的图形，与原图形相比
A．形状没有改变，大小没有改变 B．形状没有改变，大小有改变
C．形状有改变，大小没有改变 D．形状有改变，大小有改变
A
【解析】
试题分析：∵轴对称变换不改变图形的形状与大小，
∴与原图形相比，形状没有改变，大小没有改变。
故选A。 如图，正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′，下列判断错误的是（ ）．
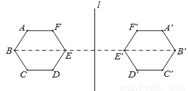
A．AB=A′B′ B．BC∥B′C′ C．直线l⊥BB′ D．∠A′=120°
B．
【解析】
试题分析：关于轴对称的两个图形沿对称轴翻折，能够重合，两个图形是全等形，对应边相等，所以A正确；C正确，因为正六边形的一个内角是120度，所以D正确．故本题选B． 下列语句中，正确的个数有（ ）
①两个关于某直线对称的图形是全等的
②两个图形关于某直线对称，对称点一定在该直线的两旁
③两个成轴对称的图形的对应点连线的垂直平分线，就是它们的对称轴
④平面内两个全等的图形一定关于某直线对称．
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】【解析】
①两个关于某直线对称的图形是全等的，此选项正确；
②两个图形关于某直线对称，对称点一定在该直线的两旁也有可能在直线上，此选项错误；
③两个成轴对称的图形的对应点连线的垂直平分线，就是它们的对称轴，此选项正确；
④平面内两个全等的图形不一定关于某直线对称，故此选项错误．
故选B． 如图，△ABC和△A′B′C′关于直线l对称，下列结论中：
①△ABC≌△A′B′C′；
②∠BAC′=∠B′AC；
③l垂直平分CC′；
④直线BC和B′C′的交点不一定在l上，
正确的有（ ）
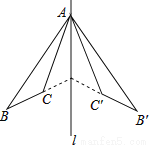
A. 4个 B. 3个 C. 2个 D. 1个
B
【解析】【解析】
∵△ABC和△A′B′C′关于直线l对称，
∴①△ABC≌△A′B′C′，正确；
②∠BAC=∠B′AC′，
∴∠BAC+∠CAC′=∠B′AC′+∠CAC′，
即∠BAC′=∠B′AC正确；
③l垂直平分CC′，正确；
④应为：直线BC和B′C′的交点一定在l上，故本小题错误．
综上所述，结论正确的是①②③共3个．
故... 已知△ABC关于直线MN对称，则下列说法错误的是（ ）
A. △ABC中必有一个顶点在直线MN上
B. △ABC中必有两个角相等
C. △ABC中，必有两条边相等
D. △ABC中必有有一个角等于60°
D
【解析】【解析】
∵△ABC关于直线MN对称，∴△ABC为等腰三角形，其对称轴为底边上的高所在的直线．
A、△ABC中必有一个顶点在直线MN上，故本选项正确；
B、△ABC中必有两个角相等，故本选项正确；
C、△ABC中，必有两条边相等，故本选项正确；
D、当该等腰三角形是等边三角形时，△ABC中有一个角等于60°，故本选项错误．
故选D． 如图，△ABC和△A′B′C′关于直线l对称，求证：△ABC≌△A′B′C′．若△ABC≌△A′B′C′，那么△ABC和△A′B′C′一定关于某条直线l对称吗？若一定请给出证明，若不一定请画出反例图。
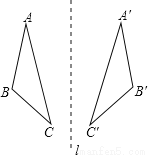
见解析
【解析】试题分析：根据轴对称的定义即可证明；举反例可以说明全等不一定轴对称．
试题解析：【解析】
∵△ABC和△A′B′C′关于直线l对称，∴△ABC和△A′B′C′能够完全重合，∴△ABC≌△A′B′C′．
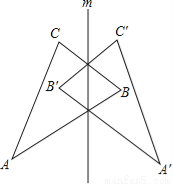
若△ABC≌△A′B′C′，△ABC和△A′B′C′不一定一定关于某条直线l对称，如图所示． 如图，△ABC和△A′B′C′关于直线m对称．
（1）结合图形指出对称点．
（2）连接A、A′，直线m与线段AA′有什么关系？
（3）延长线段AC与A′C′，它们的交点与直线m有怎样的关系？其它对应线段（或其延长线）的交点呢？你发现了什么规律，请叙述出来与同伴交流．
【解析】
（1）对称点有A和A'，B和B'，C和C'．
（2）连接A、A′，直线m是线段AA′的垂直平分线．
（3）延长线段AC与A′C′，它们的交点在直线m上，其它对应线段（或其延长线）的交点也在直线m上，
即若两线段关于直线m对称，且不平行，则它们的交点或它们的延长线的交点在对称轴上．
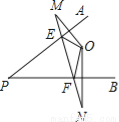
【解析】本题考查轴对称图形的定义，如果一个图形沿着一条直线对折，两侧的图形能完全重... 如图所示，已知O是∠APB内的一点，点M，N分别是O点关于PA，PB的对称点，MN与PA，PB分别相交于点E，F，已知MN=5cm，则△OEF的周长为 .
5cm．
【解析】
试题分析： ∵O是∠APB内的一点，点M，N分别是O点关于PA，PB的对称点，∴OE=ME，OF=NF，
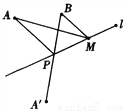
∵MN=5cm，∴△OEF的周长为：OE+EF+OF=ME+EF+NF=MN=5（cm）．故答案为：5cm． 已知：如图，A、B两点在直线l的同侧，点A'与A关于直线l对称，连接A'B交l于P点，若A'B＝a.
（1）求AP＋PB；
（2）若点M是直线l上异于P点的任意一点，求证：AM＋MB＞AP＋PB．
答案见解析
【解析】试题分析： 由轴对称的性质可知： 从而可求得答案；
由两点之间线段最短进行证明即可．
试题解析：(1)∵点A′与A关于直线l对称，
∴PA=PA′.
∴PA+PB=PA′+PB=A′B=a.
(2)∵点A′与A关于直线l对称，
∴MA=MA′.
∴AM+BM=MA′+MB.
由(1)可知：AP+PB=A′B
由两点之间线段...