题目内容
已知△ABC关于直线MN对称，则下列说法错误的是（ ）
A. △ABC中必有一个顶点在直线MN上
B. △ABC中必有两个角相等
C. △ABC中，必有两条边相等
D. △ABC中必有有一个角等于60°
D
【解析】【解析】
∵△ABC关于直线MN对称，∴△ABC为等腰三角形，其对称轴为底边上的高所在的直线．
A、△ABC中必有一个顶点在直线MN上，故本选项正确；
B、△ABC中必有两个角相等，故本选项正确；
C、△ABC中，必有两条边相等，故本选项正确；
D、当该等腰三角形是等边三角形时，△ABC中有一个角等于60°，故本选项错误．
故选D．
练习册系列答案
阅读快车系列答案
相关题目
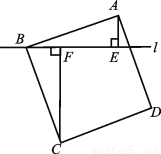
如图，过正方形ABCD的顶点B作直线l，过点A，C作l的垂线，垂足分别为点E，F．若AE＝2，CF＝6，则AB的长度为 ．
．
【解析】
试题分析：∵四边形ABCD是正方形，
∴∠CBF+∠FBA=90°，∠CBF+∠BCF=90°，
∴∠BCF=∠ABE，
∵∠AEB=∠BFC=90°，AB=BC，
∴△ABE≌△BCF（AAS）
∴AE=BF，BE=CF，
∴AB=．
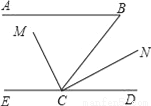
故答案是． 如图，已知AB∥CD，∠B=65°，CM平分∠BCE，∠MCN=90°，求∠DCN的度数．
32.5°．
【解析】试题分析：已知AB∥CD，∠B=65°，根据平行线的性质可求得∠BCE =115°；再由角平分线的定义求得∠ECM的度数，即可求得∠DCN的度数．
试题解析：
∵ AB∥CD，∴ ∠B+∠BCE =180°（两直线平行，同旁内角互补）
∵ ∠B =65°，∴ ∠BCE =115°
∵ CM平分∠BCE，∴ ∠ECM=∠BCE =57.5°
... 一个角的余角比这个角的补角小_____.
90°
【解析】设这个角是x°，由题意得
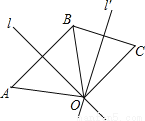
（180°- x°）-（90°- x°）=90°. 如图，l是线段AB的对称轴，l′是线段BC的对称轴，l和l′相交于点O．OA与OC相等吗？为什么？
相等，理由见解析
【解析】试题分析：由轴对称的性质即可证明．
试题解析：【解析】
∵l是线段AB的对称轴，∴OA=OB，
∵l′是线段BC的对称轴，∴OB=OC，
∴OA=OC． 探索:
(x-1)(x+1)=x2-1, (x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1, (x-1)(x4+x3+x2+x+1)=x5-1,
……
(1)试写出第五个等式;
(2)试求26+25+24+23+22+2+1的值;
(3)判断22 017+22 016+22 015+…+22+2+1的值的个位数字是几.
（1）x6-1（2）127（3）3
【解析】试题分析：(1)观察所给的四个等式，找出规律，写出第五个式子即可；（2）把26+25+24+23+22+2+1乘以（2-1），利用（1）所得的规律计算即可；（3）把22 017+22 016+22 015+…+22+2+1乘以（2-1），利用（1）所得的规律计算得到的结果为22 018-1，根据 （n≥1，且为整数）的末位数字4个一循环，由此计算出... 计算:
(1)-23+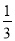
(2017+3)0-
;
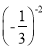(2)992-69×71;
(3)(-2+x)(-2-x);
(4)(m+2)2(m-2)2(m2+4)2;
(5)(a+b-c)(a-b+c);
(6)(3x-2y+1)2.
(1)-16 (2)4902(3)4-x2(4)m8-32m4+256(5)a2-b2-c2+2bc(6) 9x2+4y2-12xy+6x-4y+1
【解析】试题分析：（1）根据实数的运算顺序依次计算即可；（2）把99化为100-1，把69化为70-1,71化为70+1，再利用完全平方公式和平方差公式进行计算即可；（3）直接利用平方差公式计算即可；（4）逆用积的乘方的运算法则后利用平方差公式... 花粉的质量很小，一粒某种植物花粉的质量约为0.000 037 mg，已知1 g＝1 000 mg，那么0.000 037 mg用科学记数法表示为( )
A. 3.7×10－5 g B. 3.7×10－6 g C. 3.7×10－7 g D. 3.7×10－8 g
D
【解析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定． 如果直线a⊥b，c∥b，那么a∥c。（___）
×
【解析】试题分析：在同一平面内，垂直与同一条直线的两直线平行．故本题答案为“×”．