题目内容
探索:
(x-1)(x+1)=x2-1, (x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1, (x-1)(x4+x3+x2+x+1)=x5-1,
……
(1)试写出第五个等式;
(2)试求26+25+24+23+22+2+1的值;
(3)判断22 017+22 016+22 015+…+22+2+1的值的个位数字是几.
（1）x6-1（2）127（3）3
【解析】试题分析：(1)观察所给的四个等式，找出规律，写出第五个式子即可；（2）把26+25+24+23+22+2+1乘以（2-1），利用（1）所得的规律计算即可；（3）把22 017+22 016+22 015+…+22+2+1乘以（2-1），利用（1）所得的规律计算得到的结果为22 018-1，根据 （n≥1，且为整数）的末位数字4个一循环，由此计算出...
如图，在Rt△ABC中，∠ACB＝90°，D是边AB的中点，BE⊥CD，垂足为点E.已知AC＝15，cosA＝
.
(1)求线段CD的长；
(2)求sin∠DBE的值．
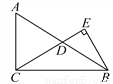
（1）CD＝；（2）sin∠DBE=.
【解析】试题分析：（1）根据直角三角形斜边上的中线等于斜边的一半，求出AB的长，即可求出CD的长；（2）由于D为AB上的中点，求出AD=BD=CD=，设DE=x，EB=y，利用勾股定理即可求出x的值，据此解答即可．
试题解析：：【解析】
（1）∵AC=15，cosA=，
∴cosA=,
∴AB=25，
∵△ACB为直角三角形，... 如果∠1与∠2互补，∠1与∠3互余，那么 ( )
A. ∠2＞∠3 B. ∠2=∠3 C. ∠2＜∠3 D. ∠2≥∠3
A
【解析】∵∠1与∠2互补，∴∠1+∠2=180°，
∵∠1与∠3互余，∴∠1+∠3=90°，
∴∠1+∠2-（∠1+∠3）=180°-90°，
∴∠2-∠3=90°，
∴∠2＞∠3．
故选A． 两条直线相交，有_____对对顶角，三条直线两两相交，有_____对对顶角.
两 六
【解析】两条直线相交，有两对对顶角，三条直线两两相交，有六对对顶角. 已知△ABC关于直线MN对称，则下列说法错误的是（ ）
A. △ABC中必有一个顶点在直线MN上
B. △ABC中必有两个角相等
C. △ABC中，必有两条边相等
D. △ABC中必有有一个角等于60°
D
【解析】【解析】
∵△ABC关于直线MN对称，∴△ABC为等腰三角形，其对称轴为底边上的高所在的直线．
A、△ABC中必有一个顶点在直线MN上，故本选项正确；
B、△ABC中必有两个角相等，故本选项正确；
C、△ABC中，必有两条边相等，故本选项正确；
D、当该等腰三角形是等边三角形时，△ABC中有一个角等于60°，故本选项错误．
故选D． (1) 已知a＋b＝7，ab＝12.求下列各式的值：
①a2－ab＋b2；②(a－b)2.
(2)已知a＝275，b＝450，c＝826，d＝1615，比较a，b，c，d的大小．
(1) ①3；②1； (2)b＞c＞a＞d.
【解析】试题分析：（1）①将a2-ab+b2化为(a+b)2-3ab，再代入求值即可；②将(a-b)2化为(a+b)2-4ab，再代入求值即可；（2）将a=275,b=450,c=826,d=1615都化为底数为2的幂，再比较大小即可.
试题解析：
(1) ①a2-ab+b2=a2+b2-ab=(a+b)2-3ab=72-3×12=1... 计算:(0.125)2 018×(22 018)3=___________.
1
【解析】原式=(0.125)2 018×82 018=(0.125×8)2 018=1. 下面两个轴对称图形分别只画出一半.请画出它的另一半.（直线l为对称轴）
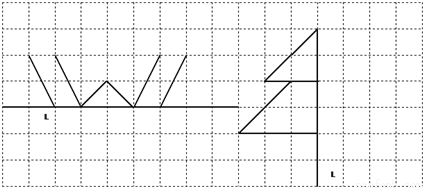
图形见解析
【解析】试题分析：从各关键点向对称轴引垂线并延长相同单位得到各点的对应点，顺次连接即可．
试题解析：【解析】
所作图形如下： 星期天，玲玲骑自行车到郊外游玩，她离家的距离与时间的关系如图所示，请根据图像回答下列问题.
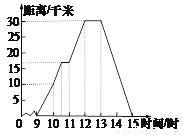
（1）玲玲到达离家最远的地方是什么时间？离家多远？
（2）她何时开始第一次休息？休息了多长时间？
（3）她骑车速度最快是在什么时候？车速多少？
（4）玲玲全程骑车的平均速度是多少？
3小时、30千米；10点休息、半小时；返回途中、15千米/小时；10千米/小时.
【解析】试题分析：本题是一道函数图象的基础题，解题的关键是通过仔细观察图象，从中整理出解题时所需的相关信息，因此本题实际上是考查同学们的识图能力．图中的点的横坐标表示时间，所以点E点距离家最远，横坐标表示距家最远的时间，纵坐标表示离家的距离；休息是路程不在随时间的增加而增加；往返全程中回来时候速度最快，用距离除...