题目内容
如图是经过轴对称变换后所得的图形，与原图形相比
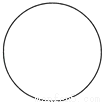
A．形状没有改变，大小没有改变 B．形状没有改变，大小有改变
C．形状有改变，大小没有改变 D．形状有改变，大小有改变
A
【解析】
试题分析：∵轴对称变换不改变图形的形状与大小，
∴与原图形相比，形状没有改变，大小没有改变。
故选A。
期末冲刺100分创新金卷完全试卷系列答案下列各组条件中，能判断两个直角三角形全等的是( )
A. 一组边对应相等 B. 两组直角边对应相等
C. 两组锐角对应相等 D. 一组锐角对应相等
B
【解析】A、两直角三角形隐含一个条件是两直角相等，现已知一组边对应相等 ，要判定两直角三角形全等，还需要一组角对应相等地或是另一组边对应相等才能进行判定，故选项错误；
B、可以利用边角边判定两三角形全等，故本选项正确；
C、两个锐角分别相等，只有角没有边，不能判定全等，此选项错误；
D、一组锐角对应相等，隐含一个条件是两直角相等，根据角对应相等，不能判定三角形全等，故选... 如图，∠1＝∠B，且∠2＝∠C，则下列结论不成立的是（ ）
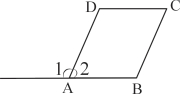
A、AD∥BC B、∠B＝∠C C、∠2＋∠B＝180° D、AB∥CD
B
【解析】
试题分析：由∠1＝∠B可得AD∥BC，再结合∠2＝∠C可得AB∥CD，再依次分析各选项即可作出判断.
∵∠1＝∠B
∴AD∥BC
∴∠2+∠B＝180°
∵∠2＝∠C
∴∠B+∠C＝180°
∴AB∥CD
故选B. 如图，直线AB、CD相交于点O，OB平分∠DOE，若∠DOE=60°，则∠AOC的度数是_____.
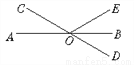
30°
【解析】因为∠BOD=45°，所以∠AOC=∠BOD=45°（对顶角相等），因为OE⊥AB，∴∠AOE=90°，所以∠COE=∠COA+∠AOE=45°+90°=135°. 如图，△ABC和△A′B′C′关于直线l对称，求证：△ABC≌△A′B′C′．若△ABC≌△A′B′C′，那么△ABC和△A′B′C′一定关于某条直线l对称吗？若一定请给出证明，若不一定请画出反例图。
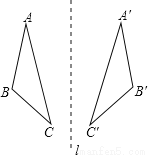
见解析
【解析】试题分析：根据轴对称的定义即可证明；举反例可以说明全等不一定轴对称．
试题解析：【解析】
∵△ABC和△A′B′C′关于直线l对称，∴△ABC和△A′B′C′能够完全重合，∴△ABC≌△A′B′C′．
若△ABC≌△A′B′C′，△ABC和△A′B′C′不一定一定关于某条直线l对称，如图所示． 先阅读再解答:我们已经知道,根据几何图形的面积关系可以说明完全平方公式,实际上还有一些等式也可以用这种方式加以说明,例如:
(2a+b)(a+b)=2a2+3ab+b2,就可以用图①的面积关系来说明.
(1)根据图②写出一个等式: ;
(2)已知等式:(x+p)(x+q)=x2+(p+q)x+pq,请你画出一个相应的几何图形加以说明.
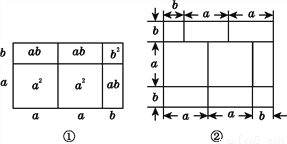
(1)(2a+b)(a+2b)=2a2+5ab+2b2(2)图形见解析
【解析】试题分析：（1）根据所给的长方形面积的两种表示法即可得等式；（2）画一个长为x+p，宽为x+q的长方形即可．
试题解析：
(1)(2a+b)(a+2b)=2a2+5ab+2b2
(2)如图.(所画图形不唯一) 2(3+1)(32+1)(34+1)-38的值是___________.
-1
【解析】原式=(3-1)(3+1)(32+1)(34+1)-38
=(32-1)(32+1)(34+1)-38
=(34-1)(34+1)-38
=38-1-38
=-1. 如图，∠XOY内有一点P，试在射线OX上找出一点M，在射线OY上找出一点N，使PM+MN+NP最短.
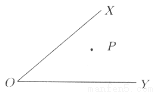
见解析
【解析】【解析】
如图所示，分别以直线OX、OY为对称轴，作点P的对称点与，
连接，分别交OX于点M，交OY于点N，则PM+MN+NP最短． 如图表示的是汽车在行驶的过程中，速度随时间变化而变化的情况．
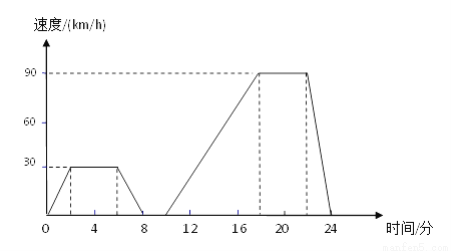
（1）汽车从出发到最后停止共经过了多少时间？它的最高时速是多少？
（2）汽车在那些时间段保持匀速行驶？时速分别是多少？
（3）出发后8分到10分之间可能发生了什么情况？
（4）用自己的语言大致描述这辆汽车的行驶情况．
（1）见解析；（2）见解析；（3）见解析；（4）见解析；
【解析】（1）汽车从出发到最后停止共经过了24min，它的最高时速是90km/h
（2）汽车大约在2分到6分，18分到22分之间保持匀速行驶，时速分别是30km/h 和90km/h
（3）出发后8分到10分速度为0，所以汽车是处于静止的。可能遇到了红灯或者障碍（或者遇到了朋友或者休息）。（答案不唯一，只要所说的情况合理即可...