��Ŀ����
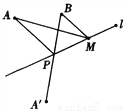
��֪����ͼ��A��B������ֱ��l��ͬ�࣬��A'��A����ֱ��l�Գƣ�����A'B��l��P�㣬��A'B��a.
��1����AP��PB��
��2������M��ֱ��l������P�������һ�㣬��֤��AM��MB��AP��PB��
 �𰸼�����
����������������� ����ԳƵ����ʿ�֪�� �Ӷ�����ô𰸣�
������֮���߶���̽���֤�����ɣ�
���������(1)�ߵ�A����A����ֱ��l�Գƣ�
��PA=PA��.
��PA+PB=PA��+PB=A��B=a.
(2)�ߵ�A����A����ֱ��l�Գƣ�
��MA=MA��.
��AM+BM=MA��+MB.
��(1)��֪��AP+PB=A��B
������֮���߶�...
�𰸼�����
����������������� ����ԳƵ����ʿ�֪�� �Ӷ�����ô𰸣�
������֮���߶���̽���֤�����ɣ�
���������(1)�ߵ�A����A����ֱ��l�Գƣ�
��PA=PA��.
��PA+PB=PA��+PB=A��B=a.
(2)�ߵ�A����A����ֱ��l�Գƣ�
��MA=MA��.
��AM+BM=MA��+MB.
��(1)��֪��AP+PB=A��B
������֮���߶�...
��ͼ��ʾ�����ı���ABCD�У�CB=CD����ABC=��ADC=90�㣬��BAC=35�㣬���BCD�Ķ���Ϊ ________�ȣ�

 110
���������ߡ�ABC=��ADC=90�㣬CB=CD����CA=CA��
���ABC�ա�ADC��
���BCA=��DCA��
�ߡ�BAC=35�㣬��ABC=90�㣬
���BCA=55�㣬
���BCD=2��BCA=110�㣬
�ʴ�Ϊ��110��
110
���������ߡ�ABC=��ADC=90�㣬CB=CD����CA=CA��
���ABC�ա�ADC��
���BCA=��DCA��
�ߡ�BAC=35�㣬��ABC=90�㣬
���BCA=55�㣬
���BCD=2��BCA=110�㣬
�ʴ�Ϊ��110�� ��������֤��������գ�
��ͼ����֪BD��AC��EF��AC��D��F�ֱ�Ϊ���㣬�ҡ�1=��4����֤����ADG=��C
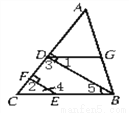
֤������BD��AC��EF��AC
���2=��3=90�㣨 ��
��BD��EF ( )
���4=_____( )
�ߡ�1=��4
���1=_____( )
��DG��BC( )
���ADG=��C( )
 ������
������������������������Ҫ��Ϥƽ���ߵ����ʺ��ж�������ȷ���������������ɣ���Ҫע��ƽ���ߵ����ʺ��ж����ۺ����ã�
�����������BD��AC��EF��AC����֪����
���2=��3=90�㣬
��BD��EF��ͬλ����ȣ���ֱ��ƽ�У���
���4=��5����ֱ��ƽ�У�ͬλ����ȣ���
�ߡ�1=��4����֪����
���1=��5��������������
��DG��BC���ڴ�����...
������
������������������������Ҫ��Ϥƽ���ߵ����ʺ��ж�������ȷ���������������ɣ���Ҫע��ƽ���ߵ����ʺ��ж����ۺ����ã�
�����������BD��AC��EF��AC����֪����
���2=��3=90�㣬
��BD��EF��ͬλ����ȣ���ֱ��ƽ�У���
���4=��5����ֱ��ƽ�У�ͬλ����ȣ���
�ߡ�1=��4����֪����
���1=��5��������������
��DG��BC���ڴ�����... ��ͼ����֪AB��CD����1=100�㣬��2=120�㣬��Ϧ�=_____.
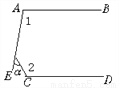
 40��
��������
�ӳ�AE��DC�ཻ�ڵ�F.
��AB��CD����1=100�㣬
���F=180��-100��=80�㣬
��Ϧ�=��2-��F=120��-80��=40��.
40��
��������
�ӳ�AE��DC�ཻ�ڵ�F.
��AB��CD����1=100�㣬
���F=180��-100��=80�㣬
��Ϧ�=��2-��F=120��-80��=40��. ��֪��AOB=40�㣬OCƽ�֡�AOB�����AOC�IJ��ǵ���_____.
 160��
��������
��OCƽ�֡�AOB����AOB=40�㣬
��,
���AOC�IJ���=180��-20��=160��.
160��
��������
��OCƽ�֡�AOB����AOB=40�㣬
��,
���AOC�IJ���=180��-20��=160��. ��ͼ����ABC�͡�A��B��C�����ֱ��l�Գƣ����н����У�
�١�ABC�ա�A��B��C�䣻
�ڡ�BAC��=��B��AC��
��l��ֱƽ��CC�䣻
��ֱ��BC��B��C��Ľ��㲻һ����l�ϣ�
��ȷ���У� ��
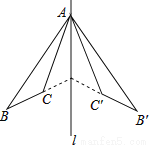
A. 4�� B. 3�� C. 2�� D. 1��
 B
����������������
�ߡ�ABC�͡�A��B��C�����ֱ��l�Գƣ�
��١�ABC�ա�A��B��C�䣬��ȷ��
�ڡ�BAC=��B��AC�䣬
���BAC+��CAC��=��B��AC��+��CAC�䣬
����BAC��=��B��AC��ȷ��
��l��ֱƽ��CC�䣬��ȷ��
��ӦΪ��ֱ��BC��B��C��Ľ���һ����l�ϣ��ʱ�С�����
����������������ȷ���Ǣ٢ڢ۹�3����
��...
B
����������������
�ߡ�ABC�͡�A��B��C�����ֱ��l�Գƣ�
��١�ABC�ա�A��B��C�䣬��ȷ��
�ڡ�BAC=��B��AC�䣬
���BAC+��CAC��=��B��AC��+��CAC�䣬
����BAC��=��B��AC��ȷ��
��l��ֱƽ��CC�䣬��ȷ��
��ӦΪ��ֱ��BC��B��C��Ľ���һ����l�ϣ��ʱ�С�����
����������������ȷ���Ǣ٢ڢ۹�3����
��... ��֪(x2��px��8)(x2��3x��q)��չ��ʽ�в���x2��x3���p��q��ֵ��
 p��3��q��1.
�����������������������ʽ�ij˷���������ɺ��ݲ������ϵ��Ϊ0��⼴��.
����������ߣ�x2+px+8����x2��3x+q��
=x4��3x3+qx2+px3��3px2+pqx+8x2��24x+8q
=x4+��p��3��x3+��q��3p+8��x2+��pq��24��x+8q��
�߳˻��в���x2��x3�
��p��3=0��q��3p+8=0��
��p=...
p��3��q��1.
�����������������������ʽ�ij˷���������ɺ��ݲ������ϵ��Ϊ0��⼴��.
����������ߣ�x2+px+8����x2��3x+q��
=x4��3x3+qx2+px3��3px2+pqx+8x2��24x+8q
=x4+��p��3��x3+��q��3p+8��x2+��pq��24��x+8q��
�߳˻��в���x2��x3�
��p��3=0��q��3p+8=0��
��p=... ��(x+m)��(x+3)�ij˻��в���x��һ�����m��ֵΪ ( )
A. �C3 B. 3 C. 0 D. 1
 A
��������(x+m)(x+3)=x2+(3+m)x+3m,
��Ϊ�������x��һ�������3+m=0,m=-3,
��ѡA.
A
��������(x+m)(x+3)=x2+(3+m)x+3m,
��Ϊ�������x��һ�������3+m=0,m=-3,
��ѡA. ���a,b,cΪͬһƽ���ڵ�3����ֱͬ�ߣ���ֱ��a��b��b��c����ôa��c. ��___��
 ��
�������������������ͬһƽ���ڣ���ֱ��ͬһ��ֱ�ߵ���ֱ��ƽ�У��ʱ����Ϊ���̡���
��
�������������������ͬһƽ���ڣ���ֱ��ͬһ��ֱ�ߵ���ֱ��ƽ�У��ʱ����Ϊ���̡��� 
