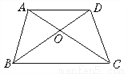
如图，AD∥BC，AC与BD相交于O，则图中相等的角有_____对.
四
【解析】∵∠AOB与∠COD是对顶角，∠AOD与∠BOC是对顶角，
∴∠AOB=∠COD，∠AOD=∠BOC.
∵AD∥BC,
∴∠CAD=∠ACB，∠ADB=∠CBD.
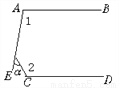
∴图中相等的角有四对. 如图，已知AB∥CD，∠1=100°，∠2=120°，则∠α=_____.
40°
【解析】
延长AE、DC相交于点F.
∵AB∥CD，∠1=100°，
∴∠F=180°-100°=80°，
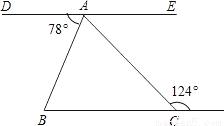
∴∠α=∠2-∠F=120°-80°=40°. 如图,DAE是一条直线,DE∥BC，则∠BAC=___度.
46°．
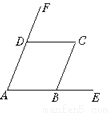
【解析】试题分析：∵DE∥BC，∴∠DAC=124°，∴∠BAC=∠DAC﹣∠DAB=124°﹣78°=46°．故答案为：46°． 如图，AB∥CD，AD∥BC，则图中与∠A相等的角有_____个.
3
【解析】∵AB∥CD，
∴∠A=∠CDF, ∠CBE=∠C;
∵AD∥BC，
∴∠A=∠CBE,
∴∠A=∠CDF=∠CBE=∠C.
∴与∠A相等的角有3个. 如图，标有角号的7个角中共有________对内错角，________对同位角，________对同旁内角.
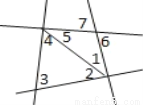
4对 2对 4对
【解析】【解析】
如图，共有4对内错角：分别是∠1和∠4，∠2和∠5，∠6和∠1，∠5和∠7；
2对同位角：分别是∠7和∠1，∠5和∠6；
4对同旁内角：分别是∠1和∠5、∠3和∠4、∠3和∠2、∠4和∠2． 如图，(1)∵∠A=_____(已知)，
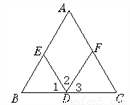
∴AC∥ED( )
(2)∵∠2=_____(已知)，
∴AC∥ED( )
(3)∵∠A+_____=180°(已知)，
∴AB∥FD( )
(4)∵AB∥_____(已知)，
∴∠2+∠AED=180°( )
(5)∵AC∥_____(已知)，
∴∠C=∠1( )
(1)∠BED 同位角相等,两直线平行?
(2)∠DFC 内错角相等，两直线平行?
(3)∠AFD 同旁内角互补，两直线平行?
(4)DF 两直线平行，同旁内角互补?
(5)ED 两直线平行，同位角相等
【解析】(1)∠BED ,同位角相等,两直线平行?
(2)∠DFC ,内错角相等，两直线平行?
(3)∠AFD ,同旁内角互补，两直线平行?
(4)... 下列语句错误的是( )
A. 锐角的补角一定是钝角 B. 一个锐角和一个钝角一定互补
C. 互补的两角不能都是钝角 D. 互余且相等的两角都是45°
B
【解析】A. ∵锐角小于90°，∴ 锐角的补角一定是钝角，故正确；
B. ∵如：30°+100°=130°，∴一个锐角和一个钝角不一定互补，故不正确；
C. ∵如果两个角都是钝角，则其和就大于180°，∴互补的两角不能都是钝角，故正确；
D. ∵互余且相等的两角都是45°，故正确；
故选B. 下列命题正确的是（ ）
A．内错角相等
B．相等的角是对顶角
C．三条直线相交 ，必产生同位角、内错角、同旁内角
D．同位角相等，两直线平行
D．
【解析】
试题分析：A．只有两直线平行，内错角才相等，故错误；
B．对顶角相等，但相等的角不一定是对顶角，故错误；
C．必须出现“三线八角”的形式，即两直线被第三条直线所截，才产生同位角，内错角，同旁内角，故错误；
D．平行线的判定定理，故正确．
故选D． 两平行直线被第三条直线所截，同位角的平分线（ ）
A. 互相重合 B. 互相平行
C. 互相垂直 D. 相交
B
【解析】如图，AB∥CD，HI与AB，CD分别交于点M、N，EM，FN分别是∠AMH，∠CNH的平分线，由AB∥CD，根据平行线的性质可得∠AMH=∠CNH，又因EM，FN分别是∠AMH，∠CNH的平分线，所以∠1= ∠AMH，∠2=∠CNH，根据等量代换可得∠1=∠2，根据同位角相等，两直线平行即可得EM∥FN，故选B. 如果∠1与∠2互补，∠1与∠3互余，那么 ( )
A. ∠2＞∠3 B. ∠2=∠3 C. ∠2＜∠3 D. ∠2≥∠3
A
【解析】∵∠1与∠2互补，∴∠1+∠2=180°，
∵∠1与∠3互余，∴∠1+∠3=90°，
∴∠1+∠2-（∠1+∠3）=180°-90°，
∴∠2-∠3=90°，
∴∠2＞∠3．
故选A．