题目内容
如图,AB∥CD,AD∥BC,则图中与∠A相等的角有_____个.
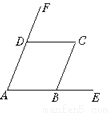
 3
【解析】∵AB∥CD,
∴∠A=∠CDF, ∠CBE=∠C;
∵AD∥BC,
∴∠A=∠CBE,
∴∠A=∠CDF=∠CBE=∠C.
∴与∠A相等的角有3个.
3
【解析】∵AB∥CD,
∴∠A=∠CDF, ∠CBE=∠C;
∵AD∥BC,
∴∠A=∠CBE,
∴∠A=∠CDF=∠CBE=∠C.
∴与∠A相等的角有3个.
练习册系列答案
相关题目
如图,MP,NQ分别垂直平分AB,AC,且BC=6 cm,则△APQ的周长为( )
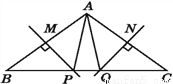
A. 12 cm B. 6 cm C. 8 cm D. 无法确定
 B
【解析】由MP、NQ分别垂直平分AB、AC,根据线段垂直平分线的性质,可得BP=AP,CQ=AQ,继而求得△APQ的周长等于BC.
【解析】
∵MP、NQ分别垂直平分AB、AC,
∴BP=AP,CQ=AQ,
∵BC=6cm,
∴△APQ的周长为:AP+PQ+AQ=BP+PQ+CQ=BC=6cm.
故选B.
B
【解析】由MP、NQ分别垂直平分AB、AC,根据线段垂直平分线的性质,可得BP=AP,CQ=AQ,继而求得△APQ的周长等于BC.
【解析】
∵MP、NQ分别垂直平分AB、AC,
∴BP=AP,CQ=AQ,
∵BC=6cm,
∴△APQ的周长为:AP+PQ+AQ=BP+PQ+CQ=BC=6cm.
故选B. 在△ABC中,AB=AC,AB的垂直平分线DE与AC所在的直线相交于点E,垂足为D,连接BE.已知AE=5,tan∠AED=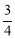 ,则BE+CE= .
,则BE+CE= .
 6或16
【解析】
试题分析:有两种情形,需要分类讨论:
①若∠BAC为锐角,如答图1所示,
∵AB的垂直平分线是DE,∴AE=BE,ED⊥AB,AD=AB。
∵AE=5,tan∠AED=,∴sin∠AED=。
∴AD=AE•sin∠AED=3。∴AB=6。
∴BE+CE=AE+CE=AC=AB=6。
②若∠BAC为钝角,如答图2所示,同理可求得:B...
6或16
【解析】
试题分析:有两种情形,需要分类讨论:
①若∠BAC为锐角,如答图1所示,
∵AB的垂直平分线是DE,∴AE=BE,ED⊥AB,AD=AB。
∵AE=5,tan∠AED=,∴sin∠AED=。
∴AD=AE•sin∠AED=3。∴AB=6。
∴BE+CE=AE+CE=AC=AB=6。
②若∠BAC为钝角,如答图2所示,同理可求得:B... ∠1=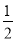 ∠2,∠1+∠2=162°,求∠3与∠4的度数.
∠2,∠1+∠2=162°,求∠3与∠4的度数.
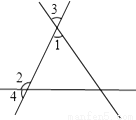
 ∠3=54°,∠4=72°
【解析】试题分析:先由∠1=∠2,∠1+∠2=162°,求出∠1和∠2的度数;再根据∠1和∠3 是对顶角,∠4和∠2为邻补角求出∠3与∠4的度数.
∵∠1=∠2,∠1+∠2=162°,
∴∠1=54°, ∠2=108°.
∵∠1和∠3是对顶角,
∴∠3=∠1=54°
∵∠2和∠4是邻补角,
∴∠4=180°-∠2=180°-10...
∠3=54°,∠4=72°
【解析】试题分析:先由∠1=∠2,∠1+∠2=162°,求出∠1和∠2的度数;再根据∠1和∠3 是对顶角,∠4和∠2为邻补角求出∠3与∠4的度数.
∵∠1=∠2,∠1+∠2=162°,
∴∠1=54°, ∠2=108°.
∵∠1和∠3是对顶角,
∴∠3=∠1=54°
∵∠2和∠4是邻补角,
∴∠4=180°-∠2=180°-10... 两平行直线被第三条直线所截,同位角的平分线( )
A. 互相重合 B. 互相平行
C. 互相垂直 D. 相交
 B
【解析】如图,AB∥CD,HI与AB,CD分别交于点M、N,EM,FN分别是∠AMH,∠CNH的平分线,由AB∥CD,根据平行线的性质可得∠AMH=∠CNH,又因EM,FN分别是∠AMH,∠CNH的平分线,所以∠1= ∠AMH,∠2=∠CNH,根据等量代换可得∠1=∠2,根据同位角相等,两直线平行即可得EM∥FN,故选B.
B
【解析】如图,AB∥CD,HI与AB,CD分别交于点M、N,EM,FN分别是∠AMH,∠CNH的平分线,由AB∥CD,根据平行线的性质可得∠AMH=∠CNH,又因EM,FN分别是∠AMH,∠CNH的平分线,所以∠1= ∠AMH,∠2=∠CNH,根据等量代换可得∠1=∠2,根据同位角相等,两直线平行即可得EM∥FN,故选B. 如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE=_____.
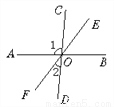
 53°
【解析】由∠BOE与∠AOF是对顶角,可得∠BOE=∠AOF,又因为∠COD是平角,可得∠1+∠2+∠AOF=180°,将∠1=95°,∠2=32°代入,即可求得∠AOF的度数,即∠BOE的度数.
53°
【解析】由∠BOE与∠AOF是对顶角,可得∠BOE=∠AOF,又因为∠COD是平角,可得∠1+∠2+∠AOF=180°,将∠1=95°,∠2=32°代入,即可求得∠AOF的度数,即∠BOE的度数. 设直线l1和直线l2平行,且l1和l2间的距离为a.如果线段AB在l1的右侧,并设AB关于l1的对称图形是A′B′,而A′B′关于l2的对称图形是A″B″(如图),那么,线段AB和A″B″有什么关系?
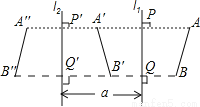
 A''B''平行且等于AB,理由见解析
【解析】试题分析:根据轴对称的性质,及在平面内垂直于同一条直线的两条直线互相平行,即可判断ABB''A''为平行四边形,继而得出答案.
试题解析:【解析】
因为l1平行于l2,并且AA″垂直于l1,当然也垂直于l2,同理BB″也垂直于l1和l2.
又在平面内垂直于同一条直线的两条直线互相平行,
所以AA″∥BB″①
另一方面,...
A''B''平行且等于AB,理由见解析
【解析】试题分析:根据轴对称的性质,及在平面内垂直于同一条直线的两条直线互相平行,即可判断ABB''A''为平行四边形,继而得出答案.
试题解析:【解析】
因为l1平行于l2,并且AA″垂直于l1,当然也垂直于l2,同理BB″也垂直于l1和l2.
又在平面内垂直于同一条直线的两条直线互相平行,
所以AA″∥BB″①
另一方面,... 先化简,再求值:-(a2-2ab)·9a2-(9ab3+12a4b2)÷3ab,其中a=-1,b=2.
 -49
【解析】试题分析:利用单项式乘以单项式的乘法法则和多项式除以单项式的除法法则计算后,合并同类项化为最简,再代入求值即可.
试题解析:
原式=-9a4+18a3b-3b2-4a3b=-9a4+14a3b-3b2.
将a=-1,b=2代入得,原式=-49.
-49
【解析】试题分析:利用单项式乘以单项式的乘法法则和多项式除以单项式的除法法则计算后,合并同类项化为最简,再代入求值即可.
试题解析:
原式=-9a4+18a3b-3b2-4a3b=-9a4+14a3b-3b2.
将a=-1,b=2代入得,原式=-49. 选择将三角形绕直线l旋转一周,可以得到如图所示主体图形的是( )
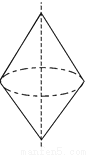
A. 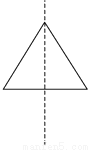 B.
B. 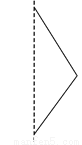 C.
C. 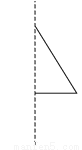 D.
D. 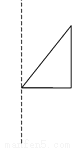
 B
【解析】解:A、C旋转一周后只有一个圆锥,B旋转后有上下两个同底的圆锥,D旋转后是一个圆柱去掉一个圆锥.故选B.
B
【解析】解:A、C旋转一周后只有一个圆锥,B旋转后有上下两个同底的圆锥,D旋转后是一个圆柱去掉一个圆锥.故选B. 
